Background

In the Bayesian analysis of sequence data, priors play an important role. When priors are not specified correctly, it may cause runs to take a long time to converge, not converge at all or cause a bias in the inferred trees and model parameters. Specifying proper priors and starting values is crucial and can be a difficult exercise in the beginning. It is not always easy to pick a proper model of tree generation (tree prior), substitution model, molecular clock model or the prior distribution for an unknown parameter.

In this tutorial we will explore how priors are selected and how molecular clock calibration works using H3N2 influenza A data from the flu virus spreading in the USA in 2009. The molecular clock model aims to estimate the substitution rate of the data. It is important to understand under which circumstances to use which model and when molecular calibration works. This will help the investigator determine which estimates of parameters can be trusted and which cannot.

---

Programs used in this exercise

BEAST2 - Bayesian Evolutionary Analysis Sampling Trees

BEAST2 is a free software package for Bayesian evolutionary analysis of molecular sequences using MCMC and strictly oriented toward inference using rooted, time-measured phylogenetic trees. This tutorial is written for BEAST v2.7.x (Bouckaert et al., 2014; Bouckaert et al., 2019).

BEAUti2 - Bayesian Evolutionary Analysis Utility

BEAUti2 is a graphical user interface tool for generating BEAST2 XML configuration files.

Both BEAST2 and BEAUti2 are Java programs, which means that the exact same code runs on all platforms. For us it simply means that the interface will be the same on all platforms. The screenshots used in this tutorial are taken on a Mac OS X computer; however, both programs will have the same layout and functionality on both Windows and Linux. BEAUti2 is provided as a part of the BEAST2 package so you do not need to install it separately.

TreeAnnotator

TreeAnnotator is used to summarise the posterior sample of trees to produce a maximum clade credibility tree. It can also be used to summarise and visualise the posterior estimates of other tree parameters (e.g. node height).

TreeAnnotator is provided as a part of the BEAST2 package so you do not need to install it separately.

Tracer

Tracer (http://beast.community/tracer) is used to summarize the posterior estimates of the various parameters sampled by the Markov Chain. This program can be used for visual inspection and to assess convergence. It helps to quickly view median estimates and 95% highest posterior density intervals of the parameters, and calculates the effective sample sizes (ESS) of parameters. It can also be used to investigate potential parameter correlations. We will be using Tracer v1.7.x.

FigTree

FigTree (http://beast.community/figtree) is a program for viewing trees and producing publication-quality figures. It can interpret the node-annotations created on the summary trees by TreeAnnotator, allowing the user to display node-based statistics (e.g. posterior probabilities). We will be using FigTree v1.4.x.

---

Practical: H3N2 flu dynamics - Heterochronous data

In this tutorial, we will estimate the rate of evolution from a set of virus sequences that have been isolated either at one point in time (homochronous data) or at different points in time (heterochronous or time-stamped data). We use the hemagglutinin (HA) gene of the H3N2 strain spreading across America alongside the pandemic H1N1 virus in 2009 (CDC, 2009/2010).

The aim of this tutorial is to obtain estimates for the:

• rate of molecular evolution
• phylogenetic relationships with measures of internal node heights
• date of the most recent common ancestor of the sampled virus sequences.

The more general aim of this tutorial is to:

• understand how to set priors and why this is important
• understand why and when the rate of evolution can be estimated from the data.

After completing this tutorial you should be able to:

• set up and run a BEAST2 XML file with heterochronous or homochronous data
• install and use a BEAST2 package
• decide if an MCMC chain has converged or not
• identify parameter correlations

The data

Before we can start we need to download the input data for the tutorial. The full heterochronous dataset contains an alignment of 139 HA sequences 1738 nucleotides long. The samples were obtained from California between April and June 2009 (file named InfluenzaAH3N2_HAgene_2009_California_heterochronous.nexus). The homochronous data is a subset of the heterochronous data, consisting of an alignment of 29 sequences of 1735 nucleotides all sampled on April 28, 2009 (file named InfluenzaAH3N2_HAgene_2009_California_homochronous.nexus).

Downloading the input data

Links to the alignment files, InfluenzaAH3N2_HAgene_2009_California_heterochronous.nexus and InfluenzaAH3N2_HAgene_2009_California_homochronous.nexus, are on the left-hand panel, under the heading Data. Right-click on the link and select “Save Link As…“ (Firefox and Chrome) or “Download Linked File As…“ (Safari) and save the file to a convenient location on your local drive. Note that some browsers will automatically change the extension of the file from .nexus to .nexus.txt. If this is the case, simply rename the file again.

Alternatively, if you left-click on the link most browsers will display the alignment file. You can then press File > Save As to store a local copy of the file. Note that some browsers will inject an HTML header into the file, which will make it unusable in BEAST2 (making this the less preferable option for downloading data files).

In the same way you can also download example .xml files for the analyses in this tutorial, as well as pre-cooked output .log and .trees files. We recommend only downloading these files to check your results or if you become seriously stuck.

Creating the analysis file with BEAUti

We will use BEAUti to select the priors and starting values for our analysis and save these settings into a BEAST2 XML file.

Begin by starting BEAUti2.

Installing BEAST2 packages

Since we will be using the birth-death skyline model (BDSKY) (Stadler et al., 2013), we need to make sure it is available in BEAUti. It is not one of the default models but rather a package (also sometimes called a plug-in or an add-on). You only need to install a BEAST2 package once. After installing, if you close BEAUti, you do not have to load BDSKY again the next time you open the program. However, it is worth checking the package manager for updates to packages, particularly if you update your version of BEAST2. For this tutorial we need to ensure that we have at least BDSKY v1.5.0 installed.

Open the BEAST2 Package Manager by navigating to File > Manage Packages. (Figure 1)

Install the BDSKY package by selecting it and clicking the Install/Upgrade button. (Figure 2)

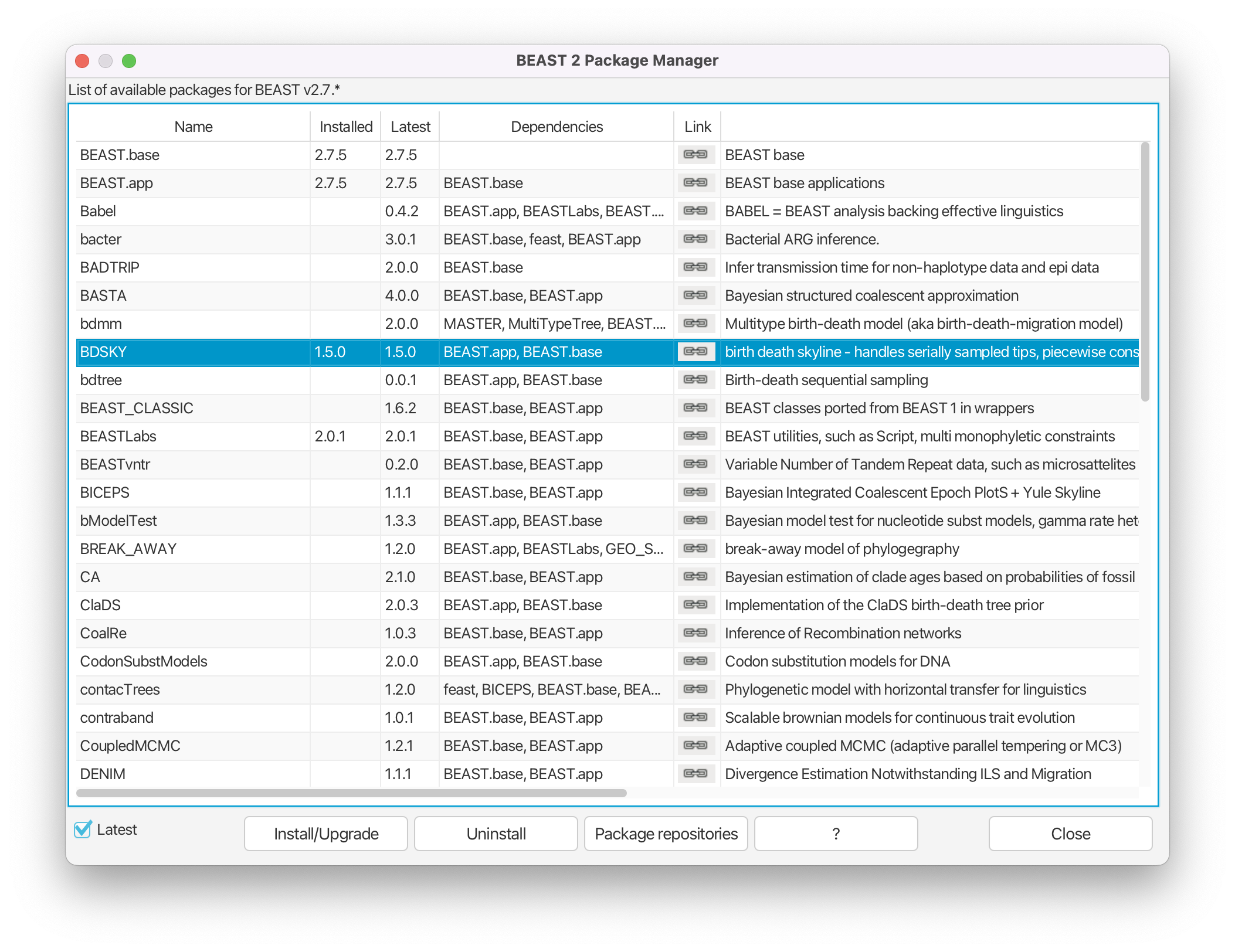
After the installation of a package, the program is on your computer, but BEAUti is unable to load the template files for the newly installed model unless it is restarted. So, let’s restart BEAUti to make sure we have the BDSKY model at hand.

Close the BEAST2 Package Manager and restart BEAUti to fully load the BDSKY package.

Importing the alignment

We will first analyse the alignment of sequences sampled through time (heterochronous sequences).

In the Partitions panel, import the nexus file with the alignment by navigating to File > Import Alignment in the menu (Figure 3) and then finding the InfluenzaAH3N2_HAgene_2009_California_heterochronous.nexus file on your computer or simply drag and drop the file into the BEAUti window.

You can view the alignment by double-clicking on the name of the alignment in BEAUti. Since we only have one partition there is nothing more we can do in the Partitions panel and proceed to specifying the tip dates.

Setting up tip dates

The heterochronous dataset contains information on the dates sequences were sampled. We want to use this information to specify the tip dates in BEAUti.

In the Tip Dates panel, click the Use tip dates option.

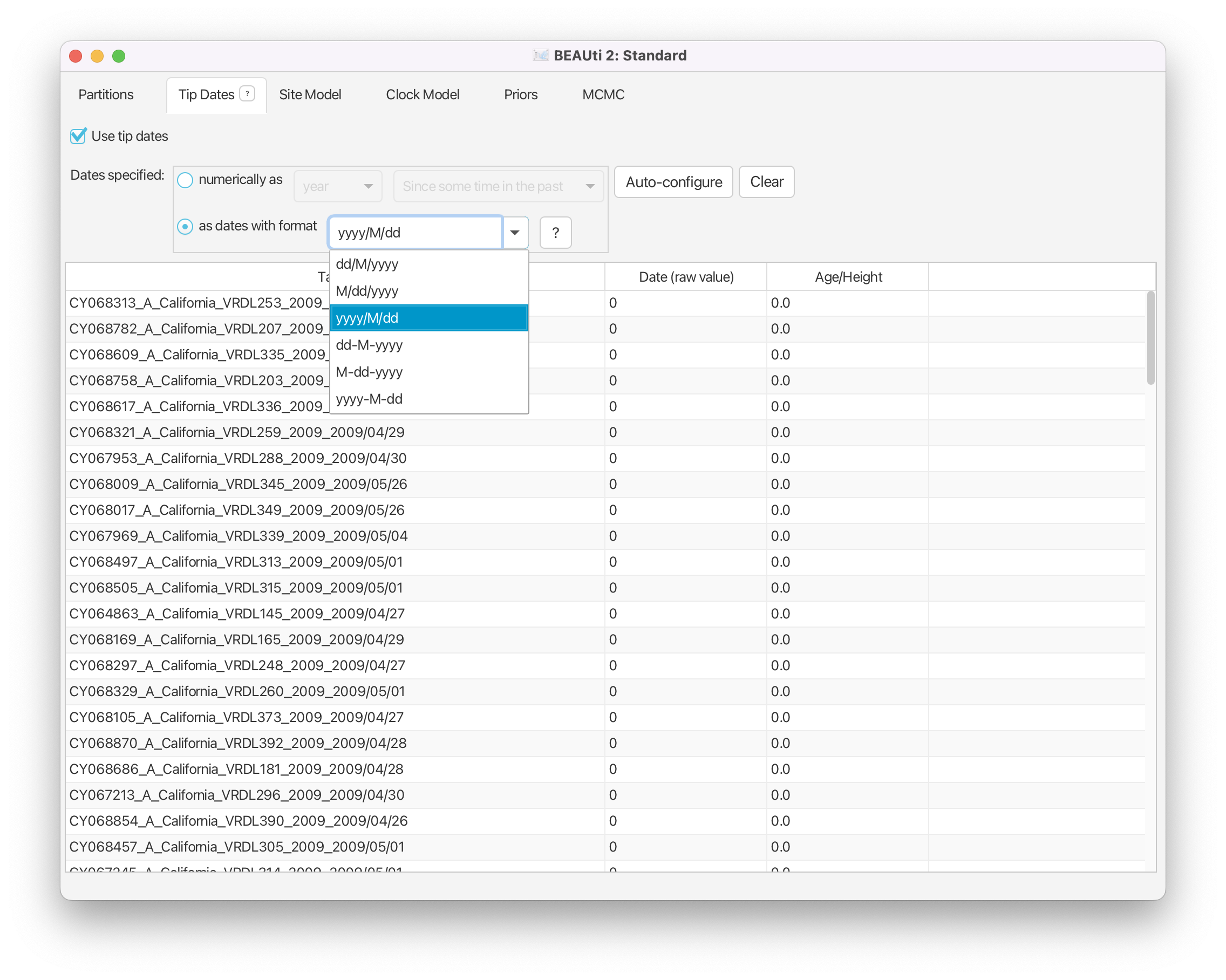
The sequence labels (headers in the FASTA file) contain sampling times specified as dates in the format year/month/day. In order for BEAST to use this information we must specify the form of this date string and tell BEAST where to find the data. To do this, first set Dates specified to the “as dates with format” option. Then open the dropdown box immediately to the right of this option and select “yyyy/M/dd” (Figure 4). This tells BEAUti that the dates are specified with a full length (4-digit) year, then the month number, then a 2-digit day, all separated by ‘/’ characters.

Set Dates specified to the option “as dates with format”, then select “yyyy/M/dd” from the list of possible date formats.

You could specify the tip dates by hand, by clicking for each row (i.e. for each sequence) into the Date (raw value) column and typing the date information in for each sequence in turn. However, this is a laborious and error-prone procedure and can take a long time to finish. Fortunately, we can use BEAUti, to read off the dates from the sequence names for us. Each sequence is named such that the expression after the last underscore character (“_”) contains the sampling date information. BEAUti can search for this expression to extract the sequence date.

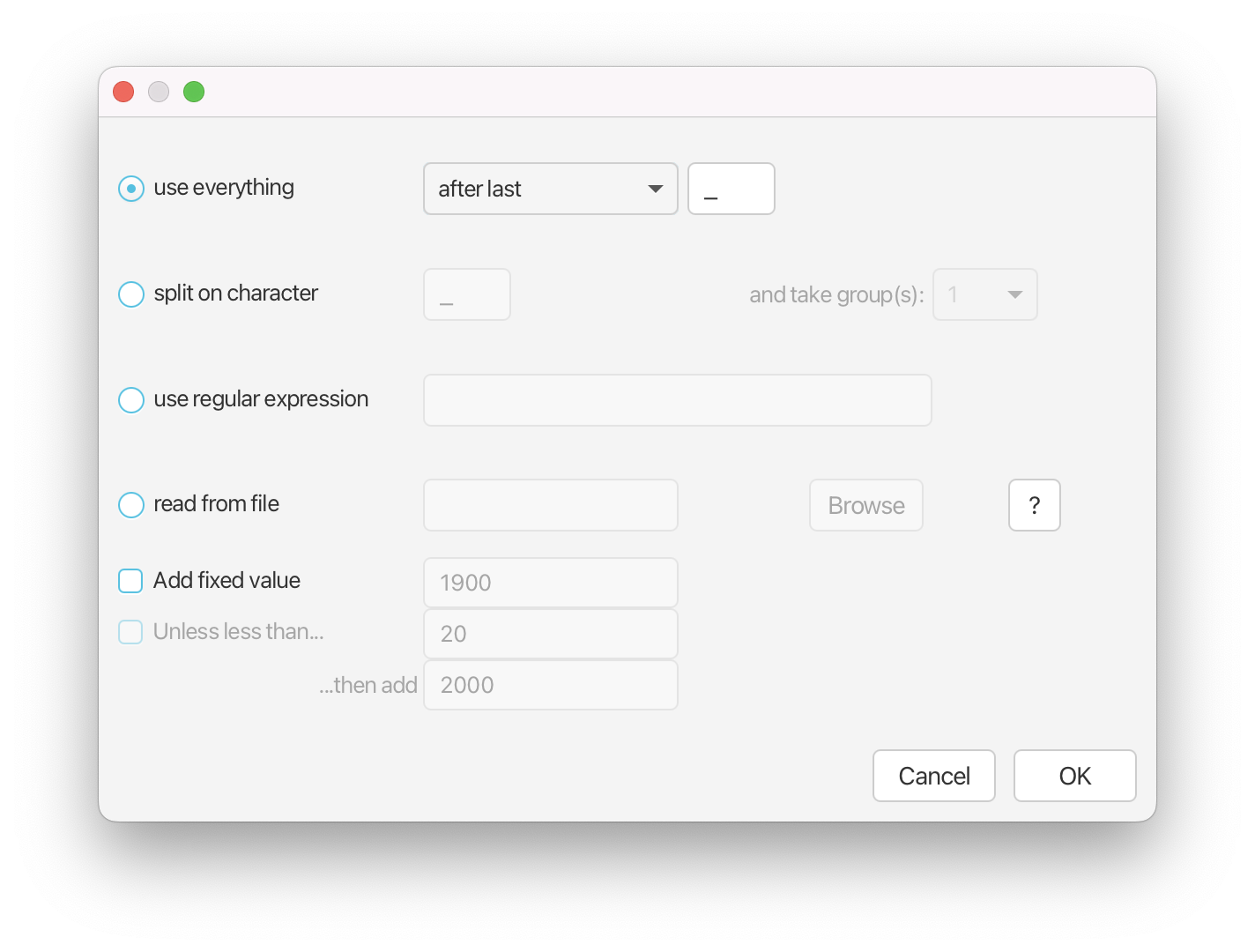
Press the Auto-configure button. A window will appear where you can specify how BEAUti can find the date of sampling of each sequence. (Figure 5)

Select use everything and specify after last _.

You should now see that the tip ages have been filled in for all of the taxa with the Date (raw value) columns showing the date strings extracted from the taxon names, and the Age/Height column showing numbers on the order of 0.1 (the age in years of each tip relative to the most recent sample). If you did everything correctly, the sequence with the most recent sampling date (2009/06/08) should have the samllest height (0.0 in this case).

Now we are done with the data specification and we are about to start specifying models and priors for the model parameters.

Specifying the Site Model

Navigate to the Site Model panel, where we can choose the model of nucleotide evolution that we want to assume to underly our dataset.

Our dataset is made of nucleotide sequences. By default there are four models of nucleotide evolution available in BEAUti2: JC69, HKY, TN93 and GTR. The JC69 model is the simplest evolutionary model. All the substitutions are assumed to happen at the same rate and all the bases are assumed to have identical frequencies, i.e. each base A, C, G and T is assumed to have an equilibrium frequency of 0.25. In the HKY model, the rate of transitions A $\leftrightarrow$ G and C $\leftrightarrow$ T is allowed to be different from the rate of transversions A $\leftrightarrow$ C, G $\leftrightarrow$ T. Furthermore, the frequency of each base can be either “Estimated”, “Empirical” or “All Equal”. When we set the frequencies to “Estimated”, the frequency of each base will be co-estimated as a parameter during the BEAST run. If we use “Empirical”, base frequencies will be set to the frequencies of each base found in the alignment. Finally, if set to “All Equal”, the base frequencies will be set to 0.25. The TN93 model is slightly more complicated than HKY, by allowing for different rates of A $\leftrightarrow$ G and C $\leftrightarrow$ T transitions. Finally, the GTR model is the most general reversible model and allows for different substitution rates between each pair of nucleotides as well as different base frequencies, resulting in a total of 9 free parameters.

Topic for discussion: Which substitution model may be the most appropriate for our dataset and why?

Since we do not have any extra information on how the sequences evolved, the decision is not clear cut. The best would be to have some independent information on what model fits the influenza data the best. Alternatively, one could perform model comparison, or apply reversible jump MCMC (see for example the bModelTest and substBMA packages) to choose the best model. Let’s assume, we have done some independent data analyses and found the HKY model to fit the influenza data the best. In general, this model captures the major biases that can arise in the analysis of nucleotide data.

Now we have to decide whether we want to assume all of the sites to have been subject to the same substitution rate or if we want to allow for the possibility that some sites are evolving faster than others. For this, we choose the number of gamma rate categories. This model scales the substitution rate by a factor, which is defined by a Gamma distribution. If we choose to split the Gamma distribution into 4 categories, we will have 4 possible scalings that will be applied to the substitution rate. The probability of a substitution at each site will be calculated under each scaled substitution rate (and corresponding transition probability matrix) and averaged over the 4 outcomes.

Topic for discussion: Do you think a model that assumes one rate for all the sites is preferable over a model which allows different substitution rates across sites (i.e. allows for several gamma rate categories)? Why or why not?

Once again, a proper model comparison, i.e. comparing a model without gamma rate heterogeneity to a model with some number of gamma rate categories, should ideally be done. We do not have any independent information on whether Gamma rate categories are needed or not. Thus, we take our best guess in order not to bias our analyses. Since the data are the sequences of the HA (hemagglutinin) gene of influenza, we may want to allow for variation of the substitution rates between sites. Hemagglutinin is a surface protein on the virus and is under significant evolutionary pressure from the immune system of the host organism. It is not unrealistic to assume that some sites may be under more pressure to escape from the immune system.

Let us therefore choose the HKY model with 4 gamma rate categories for the substitution rate.

Change the Gamma Category Count to 4, make sure that the estimate box next to the Shape parameter of the Gamma distribution is ticked and set Subst Model to HKY. Make sure that both Kappa (the transition/transversion rate ratio) and Frequencies are estimated. (Figure 6)

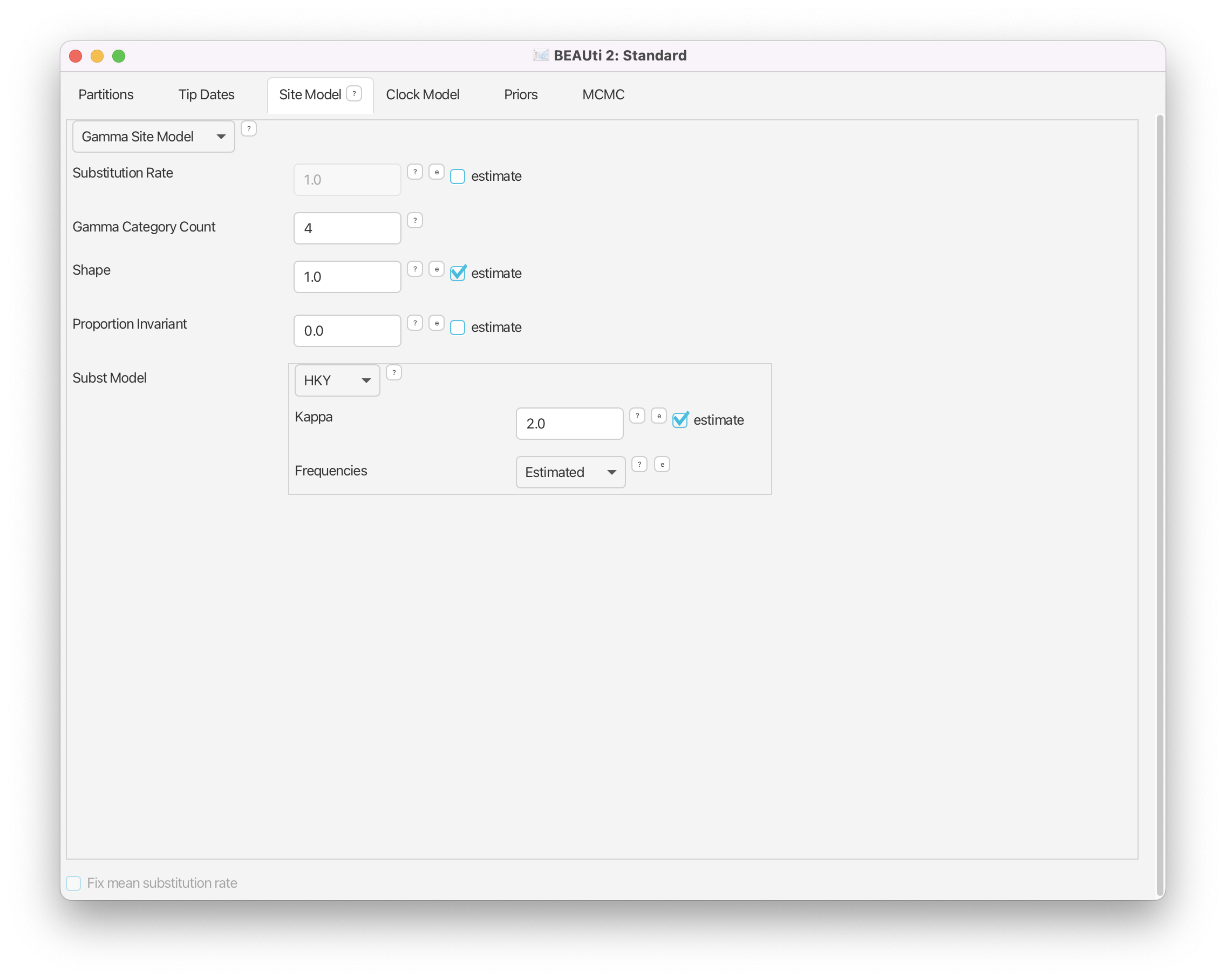
Notice that we estimate the shape parameter of the Gamma distribution as well. This is generally recommended, unless one is sure that the Gamma distribution with the shape parameter equal to 1 captures exactly the rate variation in the given dataset. Notice also, that we leave the substitution rate fixed to 1.0 and do not estimate it. In fact, the overall substitution rate is the product of the clock rate and the substitution rate (one of the two acting as a dimensionless scalar rather than a quantity measured in number of substitutions per site per time unit), and thus fixing one to 1.0 and estimating the other one allows for estimation of the overall rate of substitution. We will therefore use the clock rate to estimate the number of substitutions per site per year.

Specifying the Clock Model

Navigate to the Clock Model panel.

By default, four different clock models are available in BEAST2, allowing us to specify different models of lineage-specific substitution rate variation. The default model in BEAUti is the Strict Clock, which assumes a single fixed substitution rate across the whole tree. The other three models relax the assumption of a constant substitution rate. The Relaxed Clock Log Normal allows for the substitution rates associated with each branch to be independently drawn from a single, discretized log normal distribution (Drummond et al., 2006). Under the Relaxed Clock Exponential model, the rates associated with each branch are drawn from an exponential distribution (Drummond et al., 2006). Both of these models are uncorrelated relaxed clock models. The log normal distribution has the advantage that one can estimate its variance, which reflects the extent to which the molecular clock needs to be relaxed. In both models, BEAUti sets the Number Of Discrete Rates to -1 by default. This means that the number of bins that the distribution is divided into is equal to the number of branches. (Note that since BEAST v2.7.0 the relaxed clock models are no longer from BEAUti without installing additional packages). The last available model is the Random Local Clock which averages over all possible local clock models (Drummond & Suchard, 2010).

Topic for discussion: Which clock model may be the most appropriate for our dataset and why? (Influenza A/H3N2 HA gene sequences sampled over 3 months).

Since we are observing the sequence data from a single epidemic of H3N2 virus in humans in a single location (southwest USA), we do not have any reason to assume different substitution rates for different lineages. Thus, the most straightforward option is to choose the default Strict Clock model (Figure 7). Note however, that a rigorous model comparison would be the best way to proceed with the choice of the clock model.

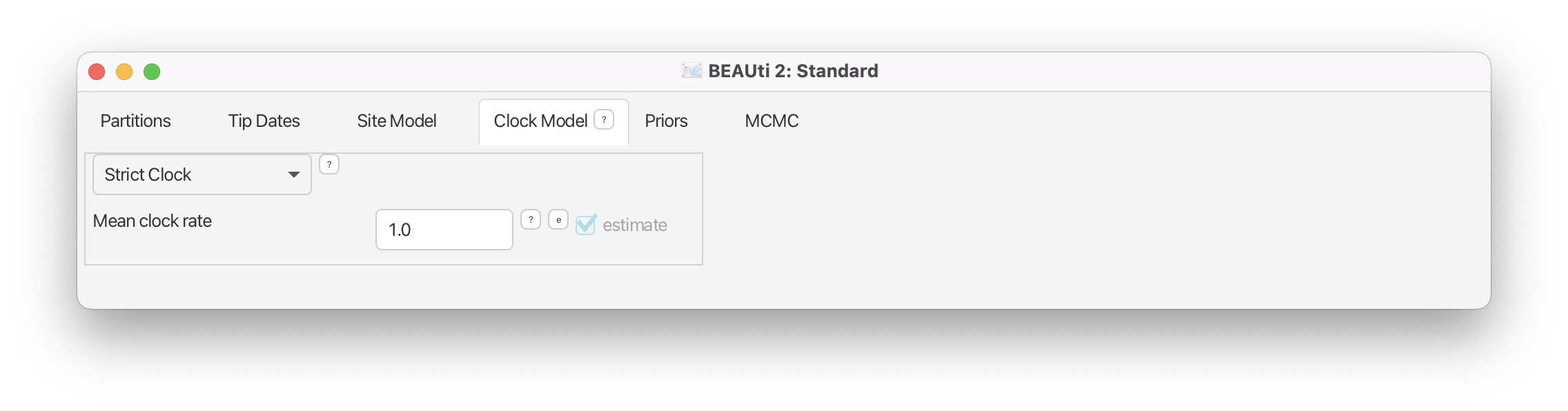
Specifying Priors

Navigate to the Priors panel.

We need to specify prior distributions for the:

• Tree
• Molecular clock model parameters
• Site model parameters

It is important to remember that a prior distribution is specified by the choice of distribution and the bounds we place on it.

Tree prior

Since the dynamics of influenza virus is likely to change due to the depletion of the susceptible population and/or the presence of resistant individuals, we choose the birth-death skyline model of population dynamics with 5 time intervals for the reproductive number, $R_e$, to capture this likely change of dynamics over time.

The birth-death skyline model adds four additional hyperparameters, for which we in turn need to specify hyperpriors:

• The effective reproductive number, $R_e$
• The becoming uninfectious rate, $\delta$
• The sampling proportion
• The origin time of the epidemic

In some cases we may fix some of the parameters of the birth-death skyline model to external estimates, in which case we would not have to specify priors for them.

$R_e$ is an important variable for the study of infectious diseases, since it defines the average number of secondary infections caused by an infected individual at a given time during the epidemic. In other words, it tells us how quickly the disease is spreading in a population. As long as $R_e$ is above 1 the epidemic is likely to continue spreading, therefore prevention efforts aim to push $R_e$ below 1. Note that as more people become infected and the susceptible population decreases, $R_e$ will naturally decrease over the course of an epidemic, however treatment, vaccinations, quarantine and changes in behaviour can all contribute to decreasing $R_e$ faster. In a birth-death process, $R_e$ is defined as the ratio of the birth (or speciation) rate and the total death (or extinction) rate. $R_e$ for any infection is rarely above 10, so we set this as the upper value for $R_e$ in our analysis.

For the Tree model, select the option Birth Death Skyline Serial.

Then, click on the arrow to the left of reproductiveNumber to open all the options for $R_e$ settings (Figure 8). Leave all the settings on the default, since the default Log Normal prior is not too strong and is centered around 1. This is exactly what we want.

Then, click on the button where it says initial = [2.0] [0.0, Infinity]. A pop-up window will show up (Figure 9).

In the pop-up window change the Upper, the upper limit of the prior distribution, from Infinity to 10 and the Dimension of $R_e$ from 10 to 5 and click OK.

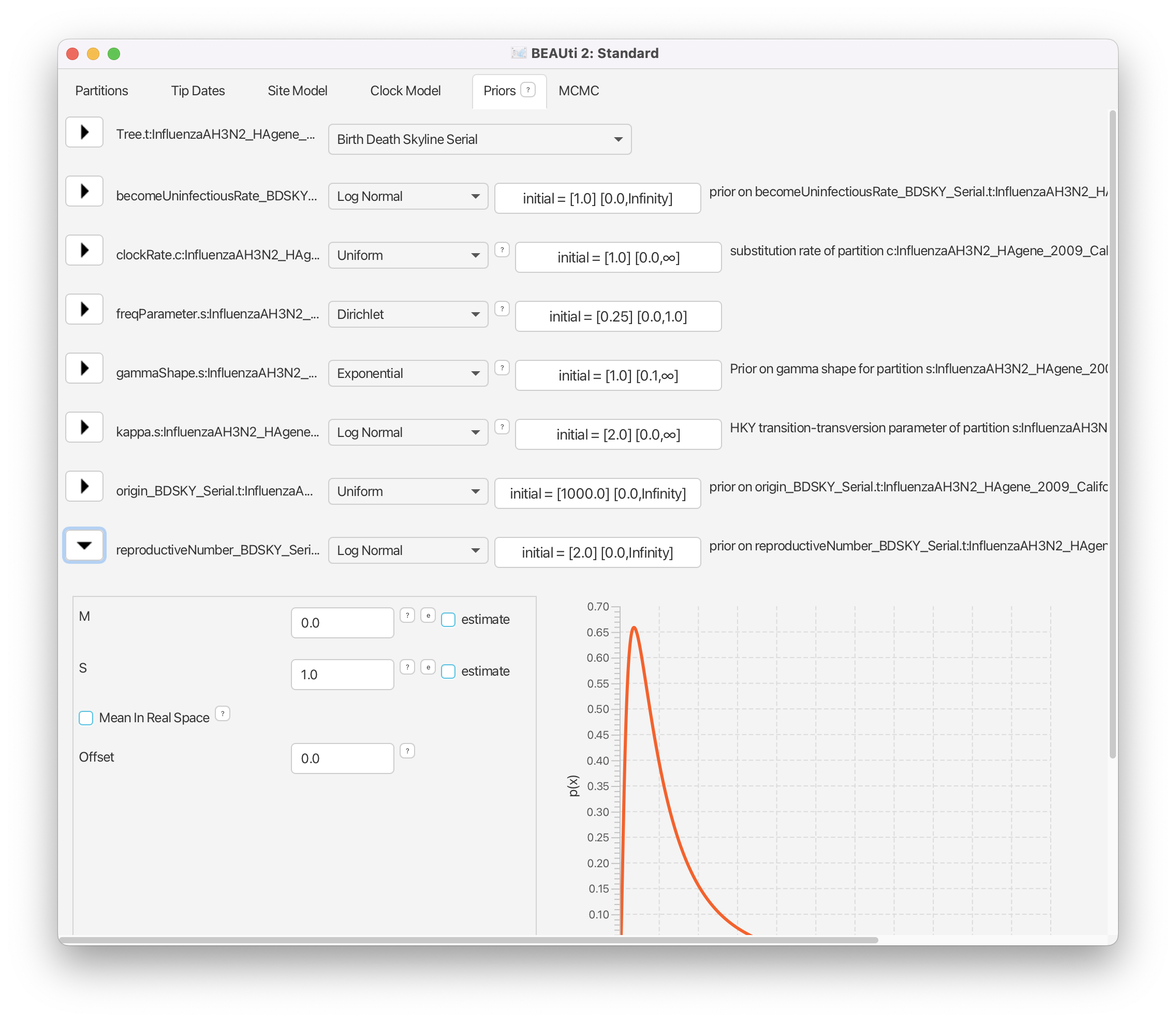
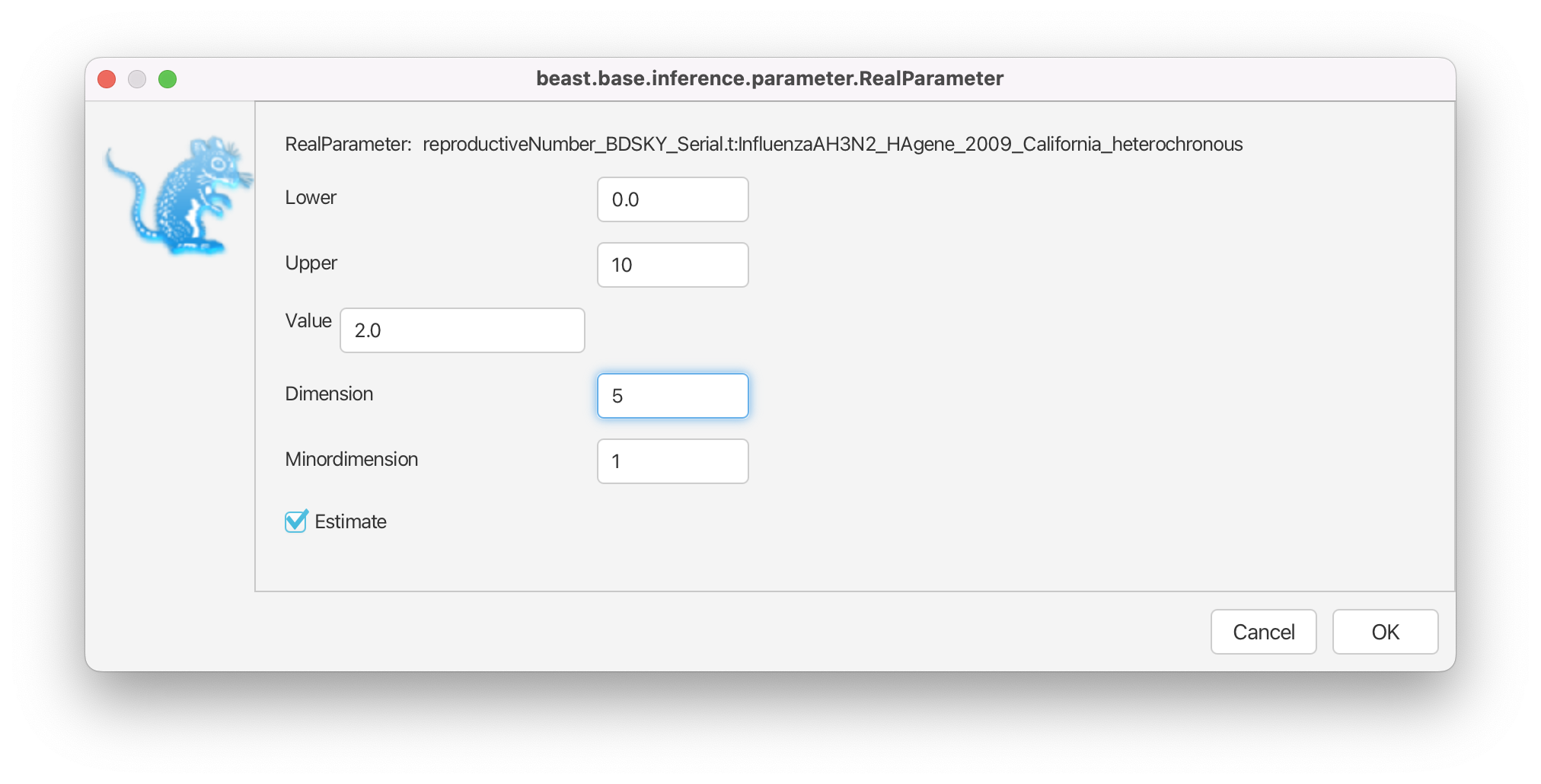
Notice that the pop-up window allows one to specify not only the Dimension but also the Minordimension. If the parameter is specified as a vector of $n$ entries, we only use the Dimension with input $n$. If the parameter is specified as an $n \times m$ matrix, we then use the Minordimension to specify the number of columns ($m$) the parameter is split into. In the birth-death skyline model, we use the parameter vector only, and thus the Minordimension always stays specified as 1. (In fact, Minordimension is only used very rarely in any BEAST2 model).

After we have specified the prior for $R_e$, the next prior that needs our attention is the becomeUninfectiousRate. This specifies how quickly a person infected with influenza recovers. From our personal experience, we would say, it takes around one week to 10 days from infection to recovery. Since the rate of becoming uninfectious is the reciprocal of the period of infectiousness this translates to a becoming uninfectious rate of 365/10=36.5 to 365/7 $\approx$ 52.14 per year (recall that we specified dates in our tree in years, and not days). Let us set the prior for becomeUninfectiousRate rate accordingly.

Click on the arrow next to becomeUninfectiousRate and change the value for M (mean) of the default log normal distribution to 52 and tick the box Mean In Real Space which allows us to specify the mean of the distribution in real space (Figure 10).

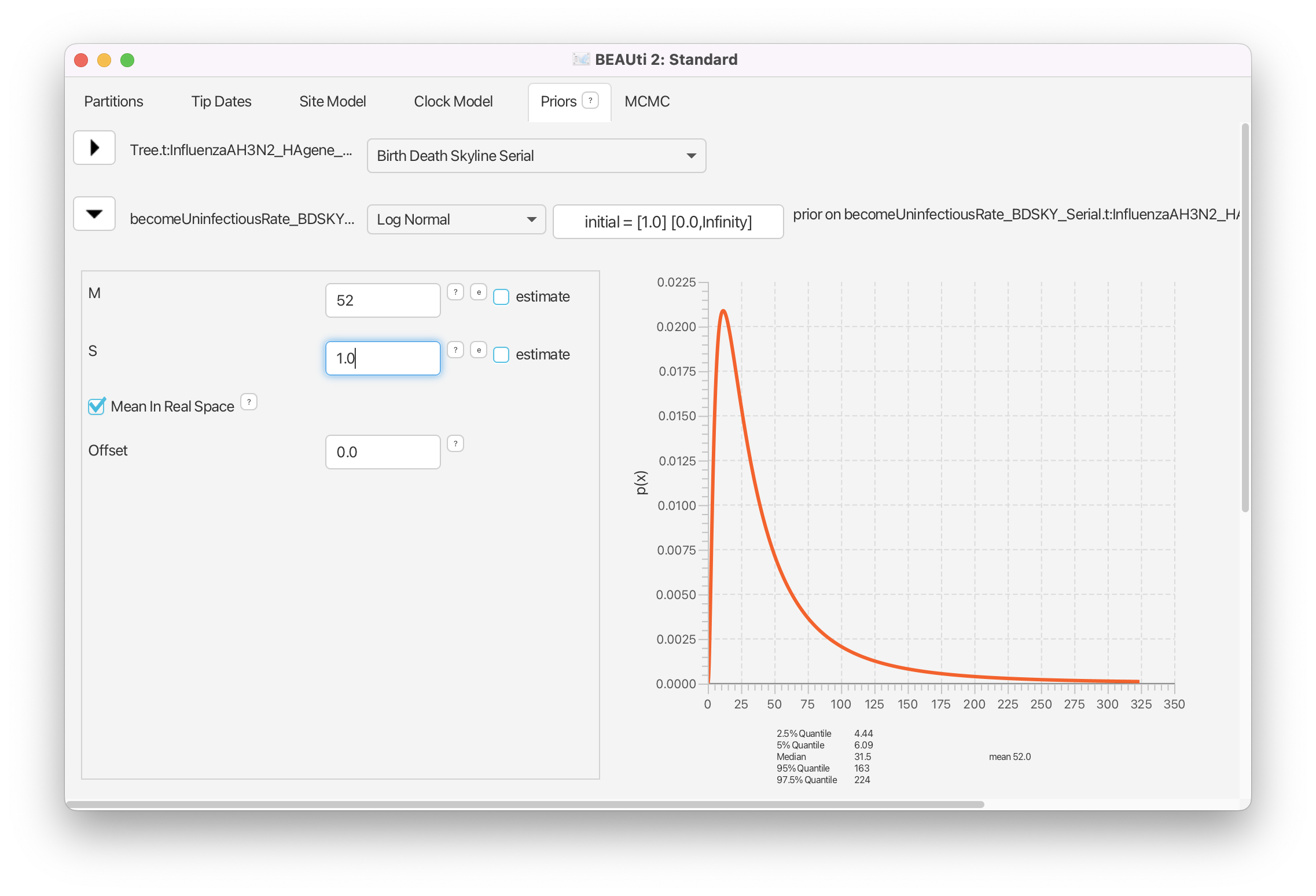
Looking at the 2.5% and 97.5% quantiles for the distribution we see that 95% of the weight of our becoming uninfectious rate prior falls between 4.44 and 224, i.e. our prior on the period of infectiousness is between $\approx$ 1.63 and 82.2 days. Thus, our prior is quite diffuse. If we wanted to use a more specific prior we could decrease the standard deviation of the distribution (the S parameter).

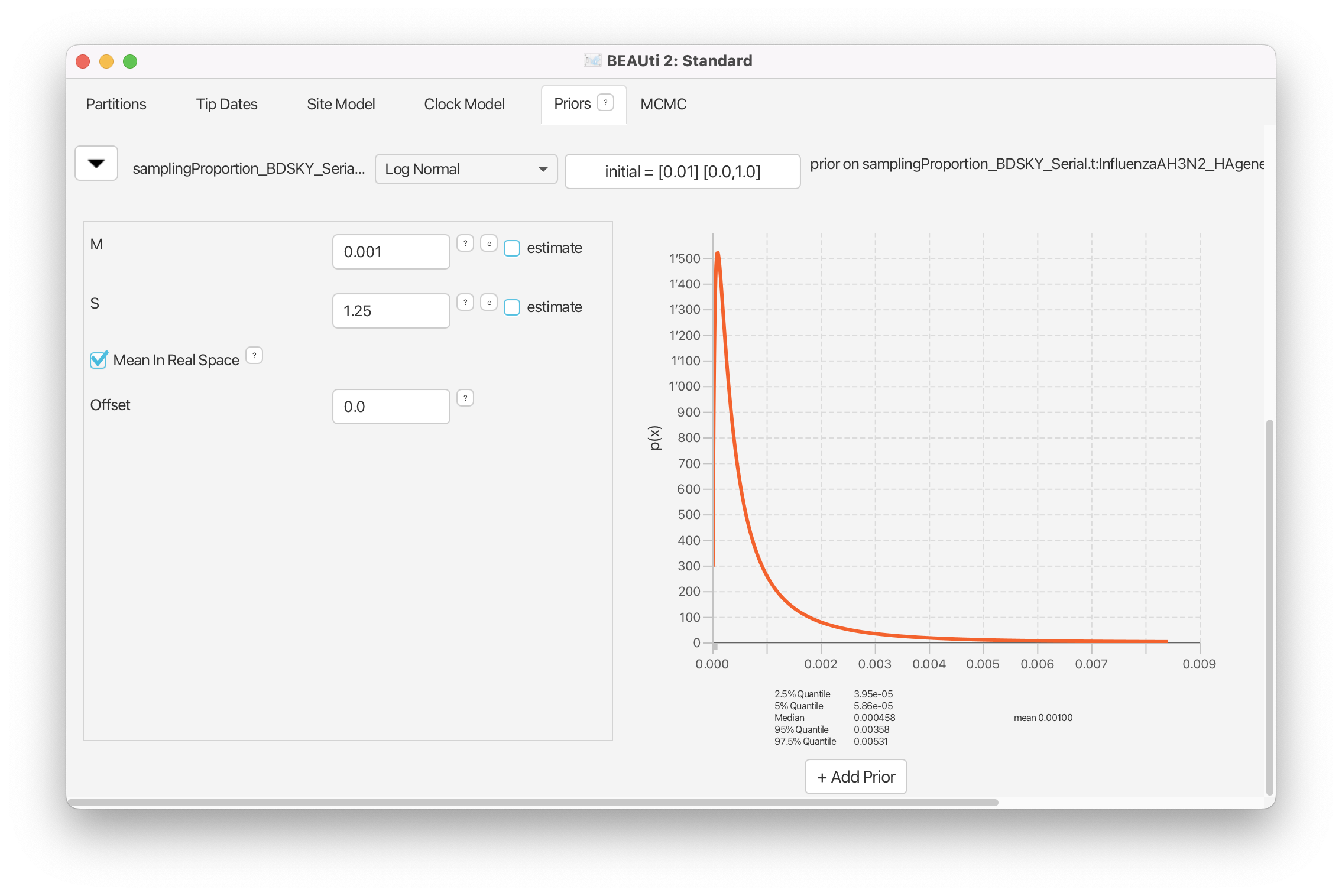
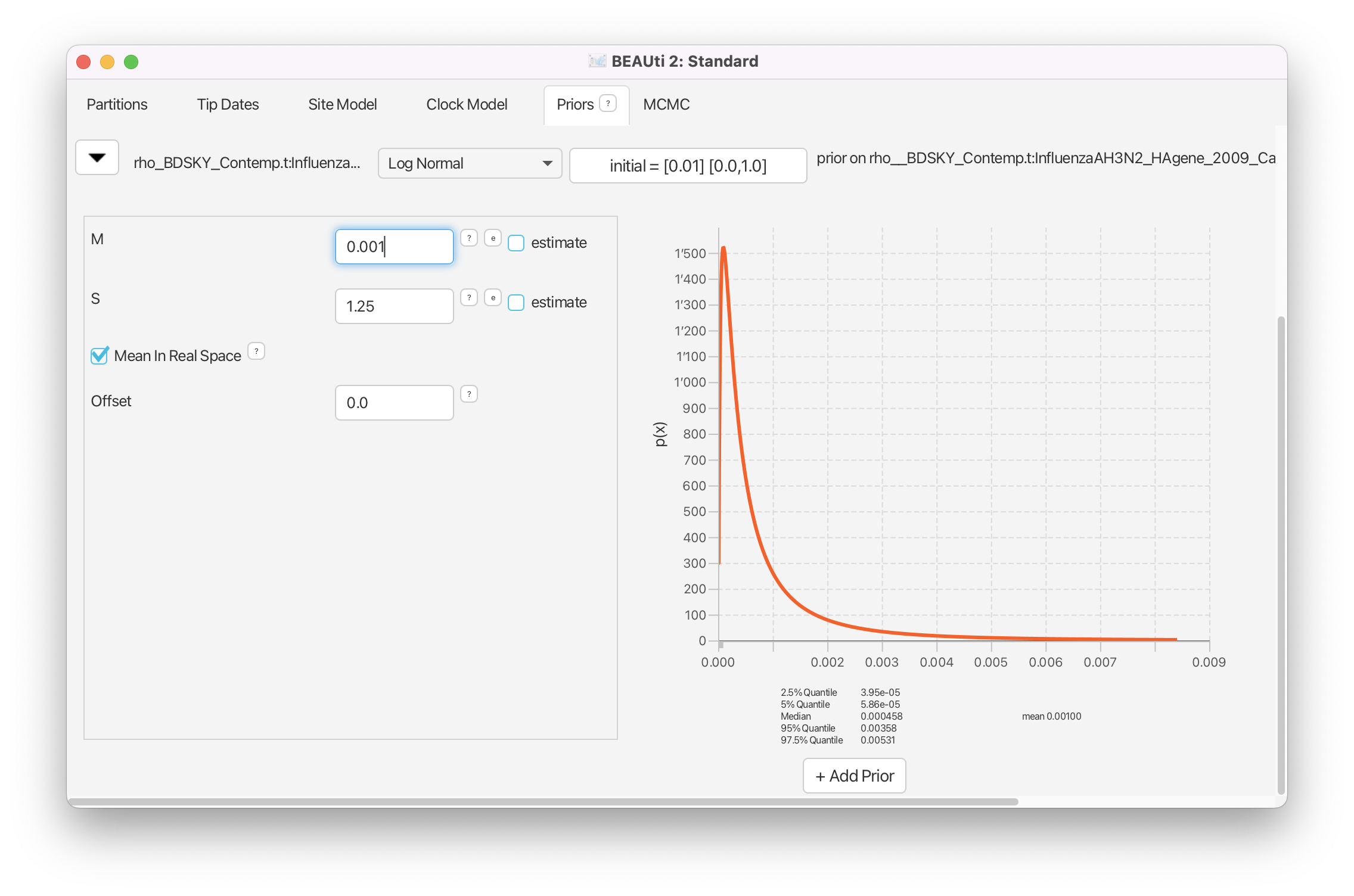
For the next parameter, the sampling proportion, we know that we certainly did not sample every single infected individual. Therefore, setting a prior close to 1 would not be reasonable. Actually, it is more reasonable to usually expect only a proportion of less than 0.1 of all flu cases to be sampled. Here, we specify something on the order of $10^{-3}$. The default prior for the sampling proportion is a Beta distribution, which is only defined between 0 and 1, making it a natural choice for proportions. However, this is not the only prior that can be used, and here we specify a log-normal distribution, while ensuring that an appropriate upper limit is set, to prevent a sampling proportion higher than 1, which is not defined.

Click on the arrow next to the samplingProportion and change the distribution from Beta to Log Normal.

Next, change the value for the M (mean) to 0.001 and tick the box Mean In Real Space (Figure 11).

Also, make sure that the Lower is set to 0.0 and the Upper is set to 1.0.

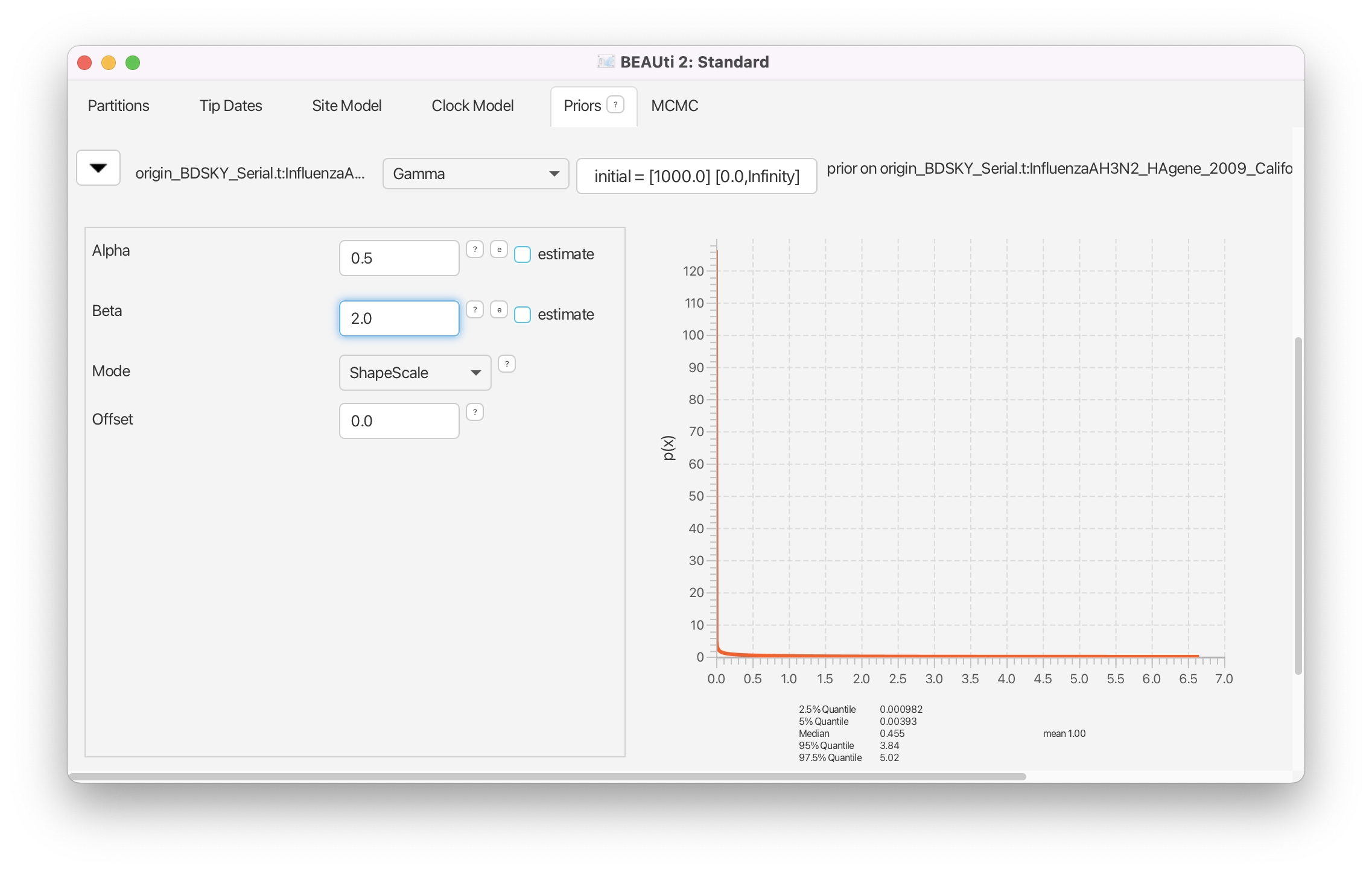
Lastly, for the origin of the epidemic, we ask ourselves whether there is any reasonable expectation we might have in terms of when the infection in California started, i.e. what is the date when the ancestor of all of the sequences first appeared.

Topic for discussion: Do you have any feeling for what the origin should/could be set to?

The data span a period of 3 months and come from a limited area; thus, it would be unreasonable to assume that a single season flu epidemic would last longer than a few months. The best guess for the origin parameter prior we could make is therefore on the order of at least 3-4, but probably no more than 6 months. We set the prior according to this expectation. (Remember that branch lengths are measured in years).

Click on the arrow next to the origin and change the prior distribution from Uniform to Gamma with Alpha parameter set to 0.5 and Beta parameter set to 2.0 (Figure 12).

Molecular clock model

We are using a strict clock model, which has only one parameter, the clock rate. This is the substitution rate, measured in substitutions per site per year (s/s/y).

Topic for discussion: What substitution rate is appropriate for viruses? More specifically, what substitution rate is expected for influenza HA genes, in your opinion?

By default, the clock rate in BEAST2 has a uniform prior between 0 and infinity. This is not only extremely unspecific, but also an improper prior (it does not integrate to 1). In general, a log-normal distribution works well for rates, since it does not allow negative values. Furthermore, it places most weight close to 0, while also allowing for larger values, making it an appropriate prior for the clock rate, which we expect to be quite low in general, but may be higher in exceptional cases. You could set your best guess as a prior by, for example, choosing a log-normal distribution centered around your best guess for the substitution rate.

Now consider the following information: Influenza virus is an RNA virus (Kawaoka, 2006) and RNA viruses in general, have a mutation rate of $\approx 10^{-3}$ substitutions per site per year (Jenkins et al., 2002).

Topic for discussion: Did you change your best guess, for the substitution rate appropriate for RNA viruses? What would it be? How would you specify the prior?

Our best guess would be to set the prior distribution peaked around $10^{-3}$ substitutions per site per year.

Change the prior for the clock rate from a Uniform to Log Normal distribution. Click on the arrow next to the clockRate and change the value for M (mean) of the default log normal distribution to 0.001 and tick the box Mean In Real Space (Figure 13).

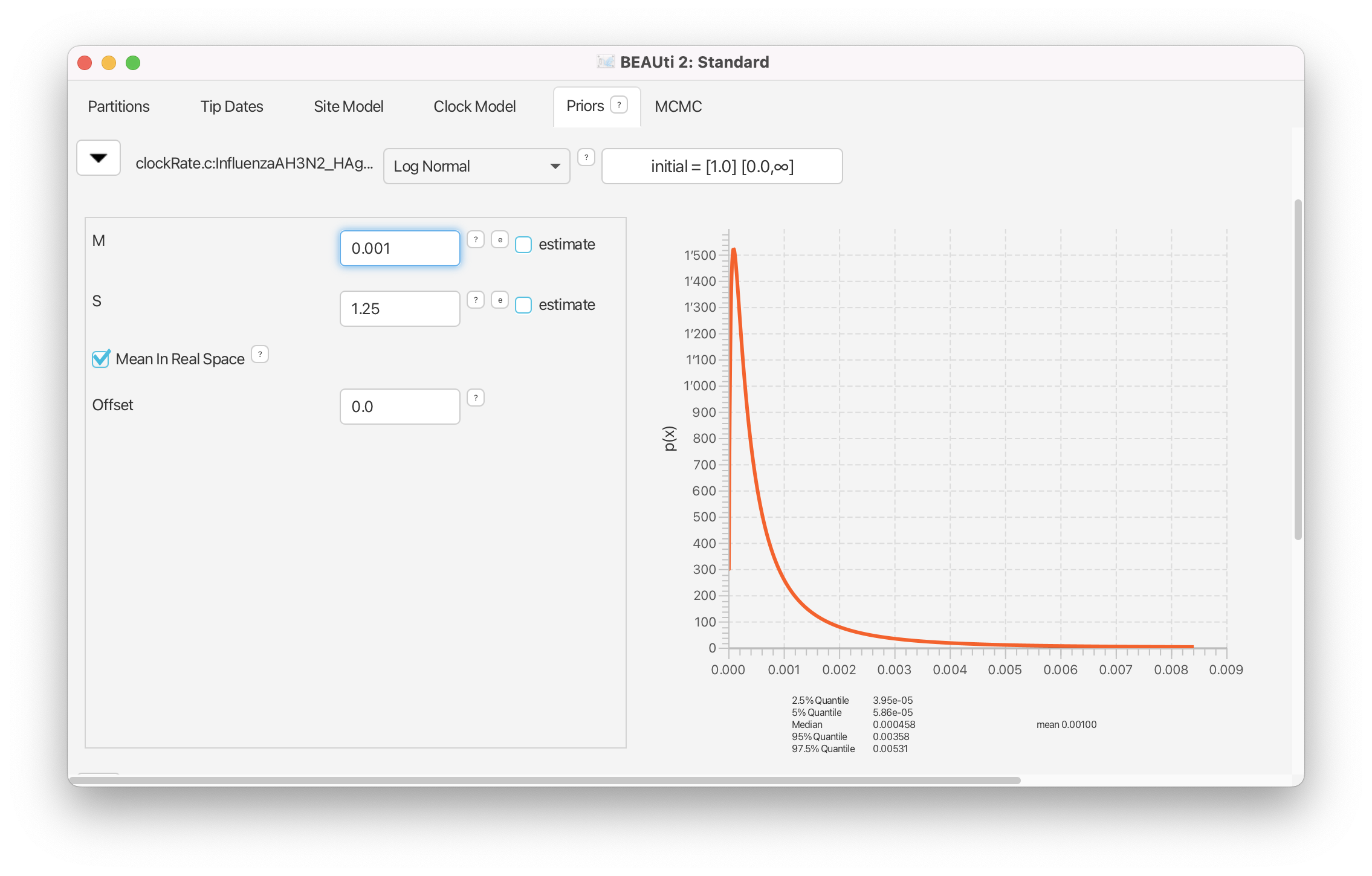
Site model

We used an HKY model, with Gamma-distributed rate heterogeneity with 4 categories and estimated equilibrium frequencies. Thus, we need to set priors for three parameters:

• The Gamma shape parameter, $\alpha$
• The transition/transversion rate ratio, $\kappa$
• The equilibrium nucleotide frequencies (actually 4 parameters)

(The default priors for site models perform well in most scenarios and in practice rarely have to be changed. However, it is important not to forgot about them!)

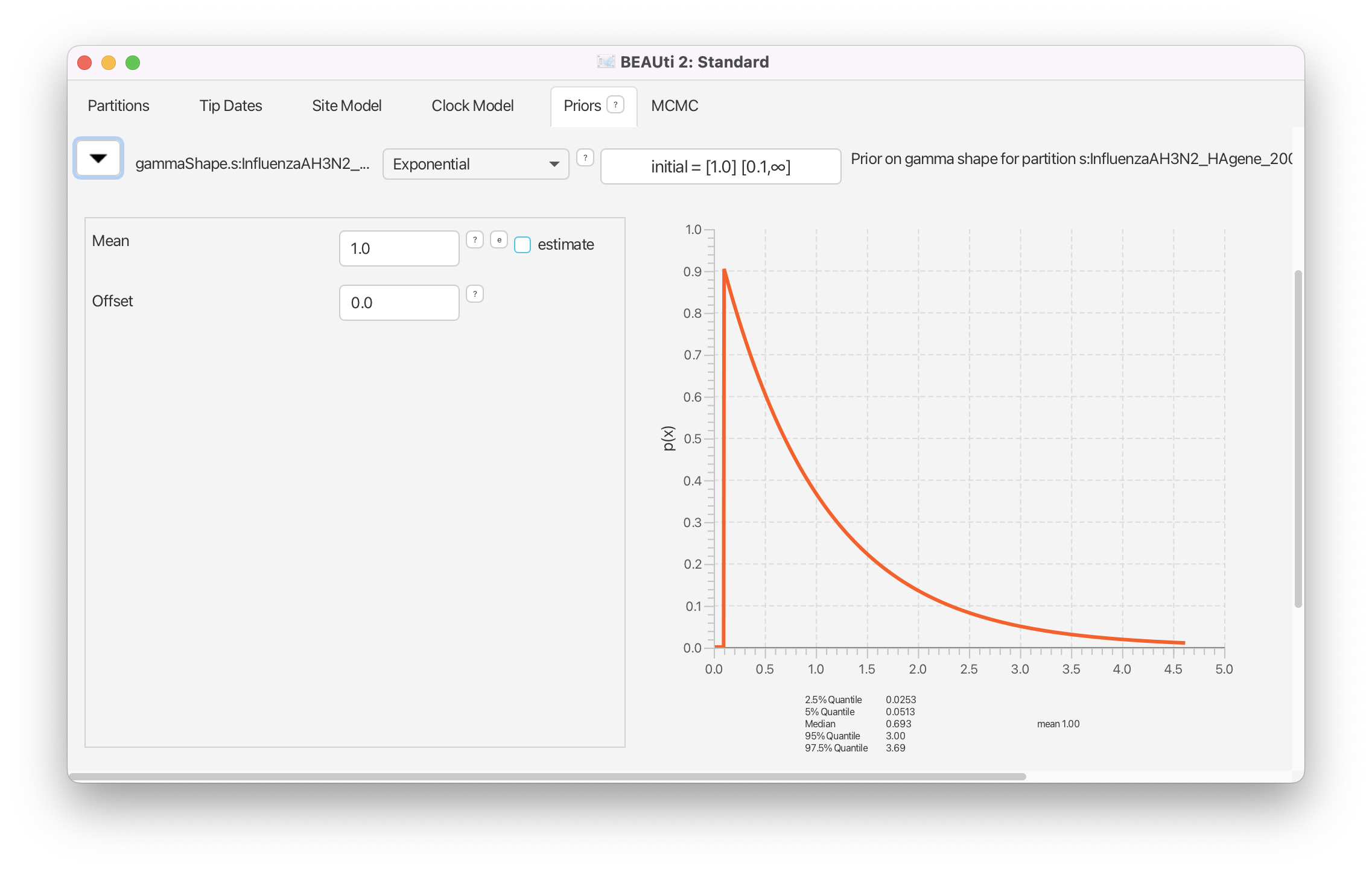
The Gamma shape parameter governs the shape of the Gamma distribution of the rates across different sites. The default setting of the Gamma shape parameter of alpha=beta=1.0 reflects our belief that on average, the rate scaler is equal to 1, i.e. on average all the sites mutate with the same substitution rate. The distribution on the gamma shape parameter allows us to deviate from this assumption. The default exponential distribution with M (mean) of 1.0 and 95%HPD of [0.0253,3.69] covers a wide range of possible shape parameters. This looks fine for our analysis, and thus, we leave the Gamma shape settings at its defaults (Figure 14).

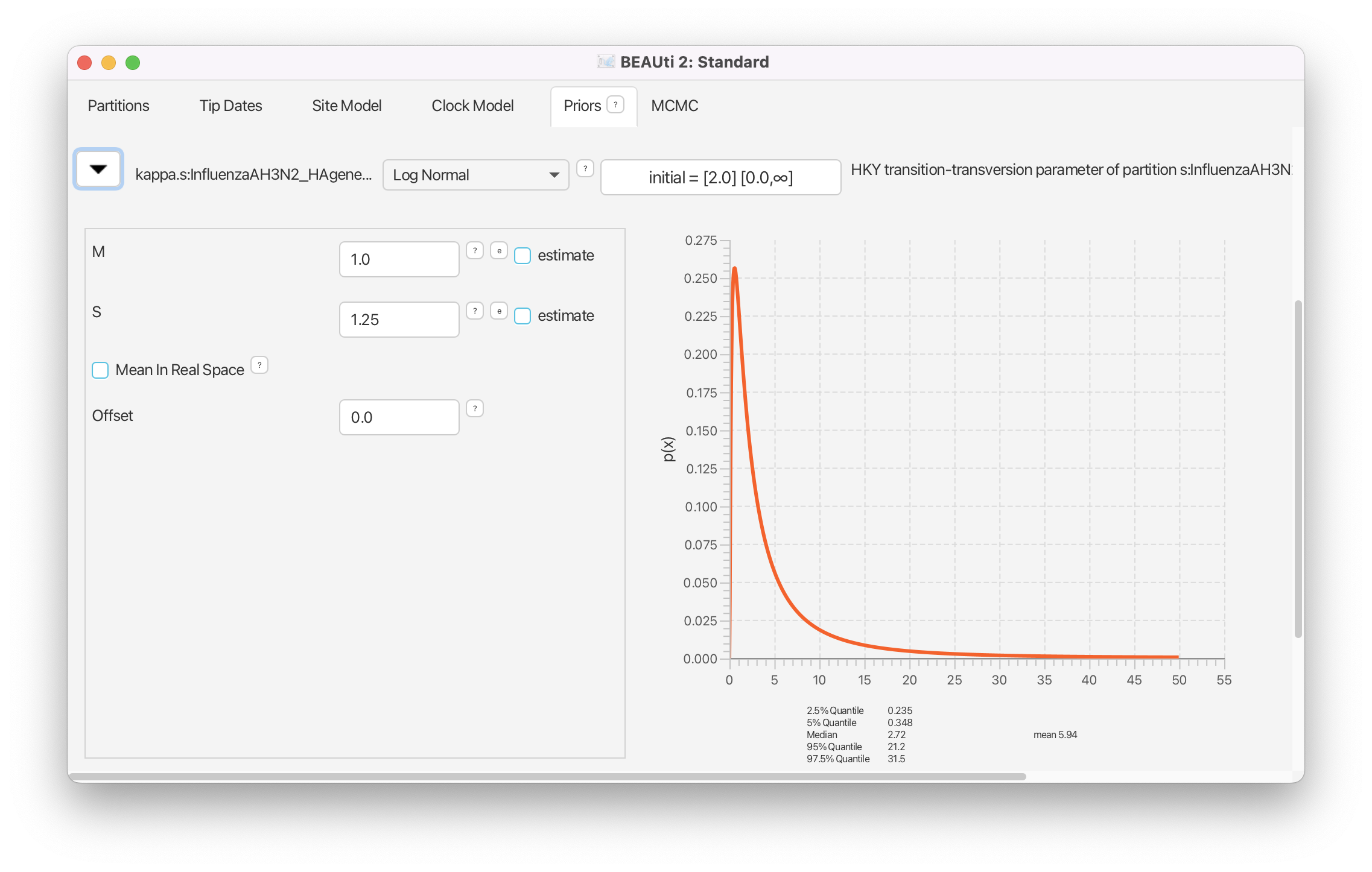
We do not have any prior information on transition-transversion rate ratio besides the fact that it is a value usually larger than 1 (transitions are more frequent than transversions). We therefore set a weakly informative prior for this parameter. The default log normal prior perfectly fits to these requirements and usually does not need to be changed (Figure 15).

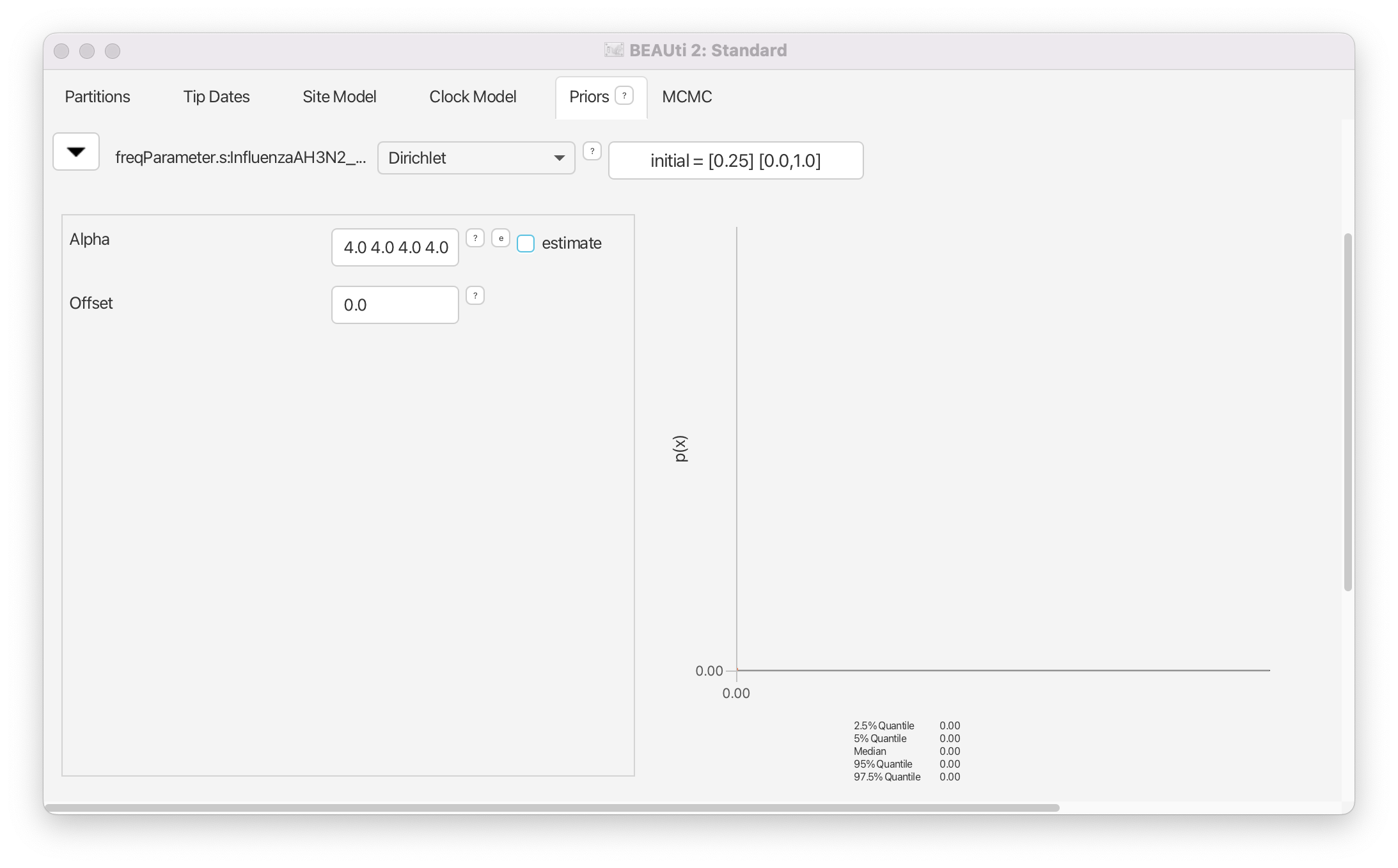
Because the equilibrium nucleotide frequencies are bounded between 0 and 1, a uniform distribution on this range or a Beta distribution may seem like natural priors for these parameters. In fact, in earlier versions of BEAST2 a uniform prior was used as the default. However, equilibrium frequencies have one additional constraint, and that is that they should sum to 1. In addition, we also know from past experience that equilibrium frequencies are rarely close to 0 (and conversely, close to 1). Thus, instead of using a univariate distribution, the default prior on equilibrium nucleotide frequencies is a Dirichlet(4,4,4,4) distribution. The Dirichlet distribution is a multivariate extension of the Beta distribution which is commonly used as a prior for categorical distributions. This distribution ensures that the frequencies sum to 1 and discourages values close to 0.

It is rarely necessary to specify a strong prior for equilibrium frequencies. Equilibrium frequencies are usually easy to infer from the data and estimates do not have a large effect on other parameters. Thus, we can leave the prior as is (Figure 16).

MCMC

Navigate to the MCMC panel.

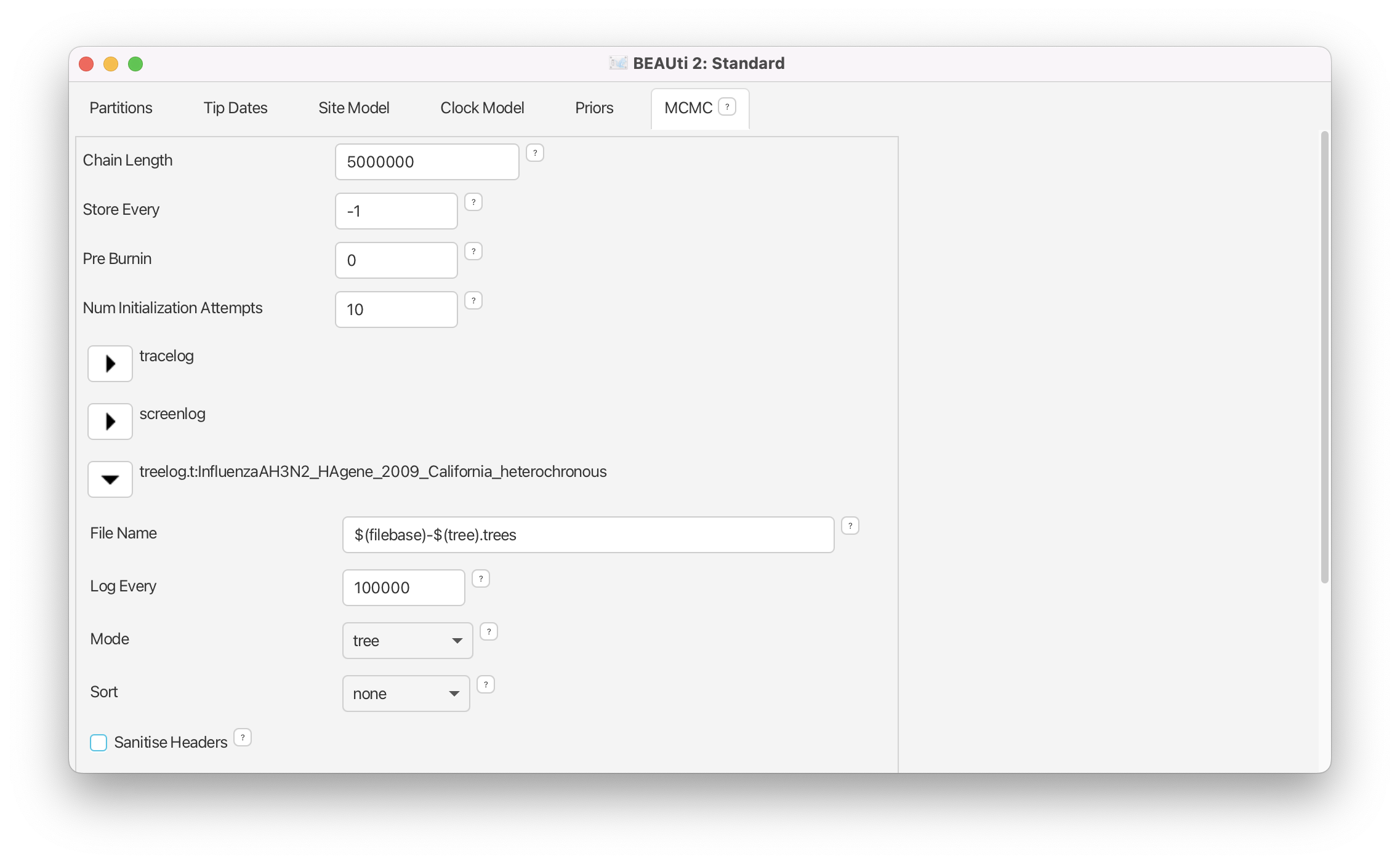
We want to shorten the chain length, in order for it to run in a reasonable time and we want to decrease the tree sampling frequency, to keep output files small.

Change the Chain Length from 10’000’000 to 5’000’000.

Click on the arrow next to the treelog and set the Log Every to 100’000 (Figure 17).

Now, all the specifications are done. We want to save and run the XML.

Save the XML file as Heterochronous.xml.

Running the analysis

Start BEAST2 and choose the file Heterochronous.xml.

If you have BEAGLE installed tick the box to Use BEAGLE library if available, which will make the run faster.

Hit Run to start the analysis.

The run should take about 15-20 minutes. While waiting for your results, you can start preparing the XML file for the homochronous data.

Analysing the results

Load the Heterochronous.log file into Tracer to check mixing and the parameter estimates.

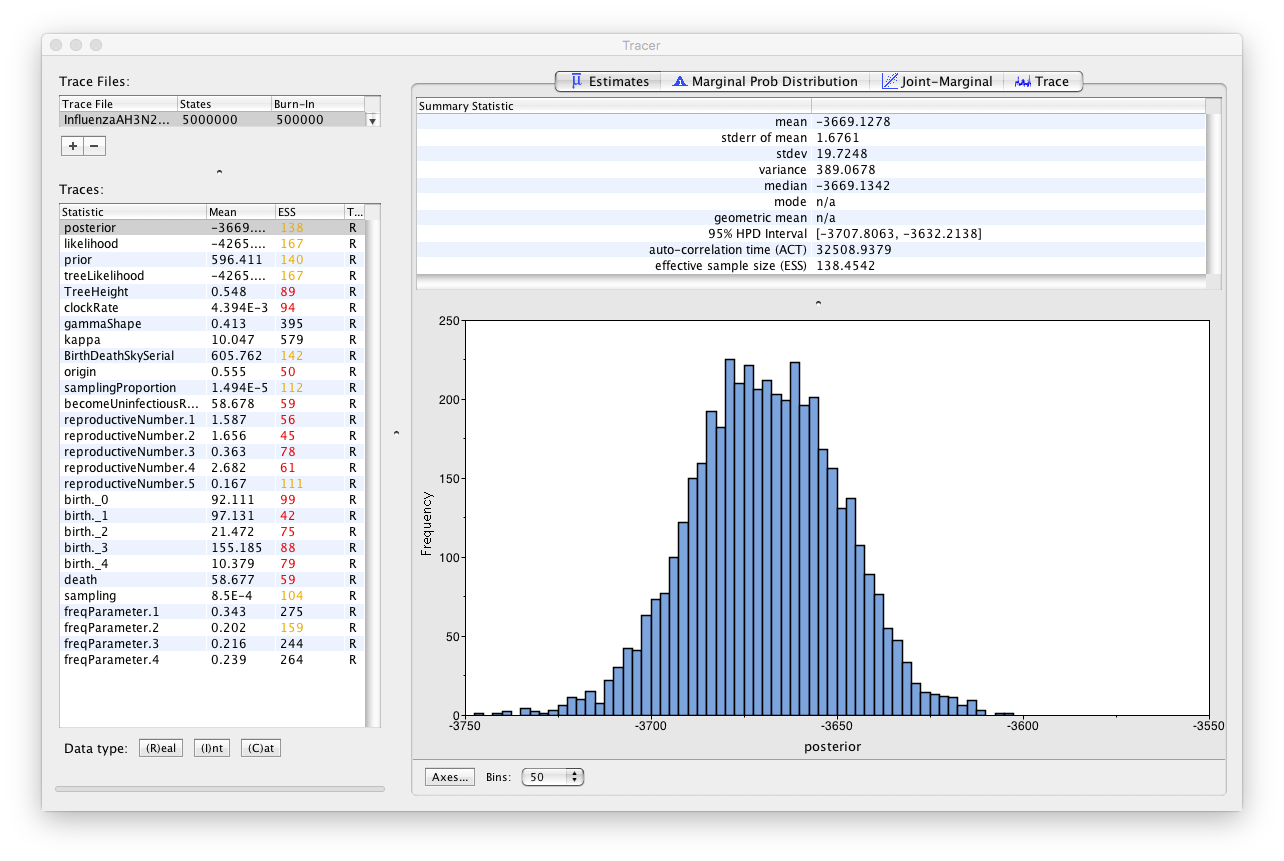
First thing you may notice is that most of the parameters have low ESS (effective sample size below 200) marked in red (< 100) and yellow (Figure 18). This is because our chain did not run long enough. However, the estimates we obtained with a chain of length 5’000’000 are very similar to those obtained with a longer chain.

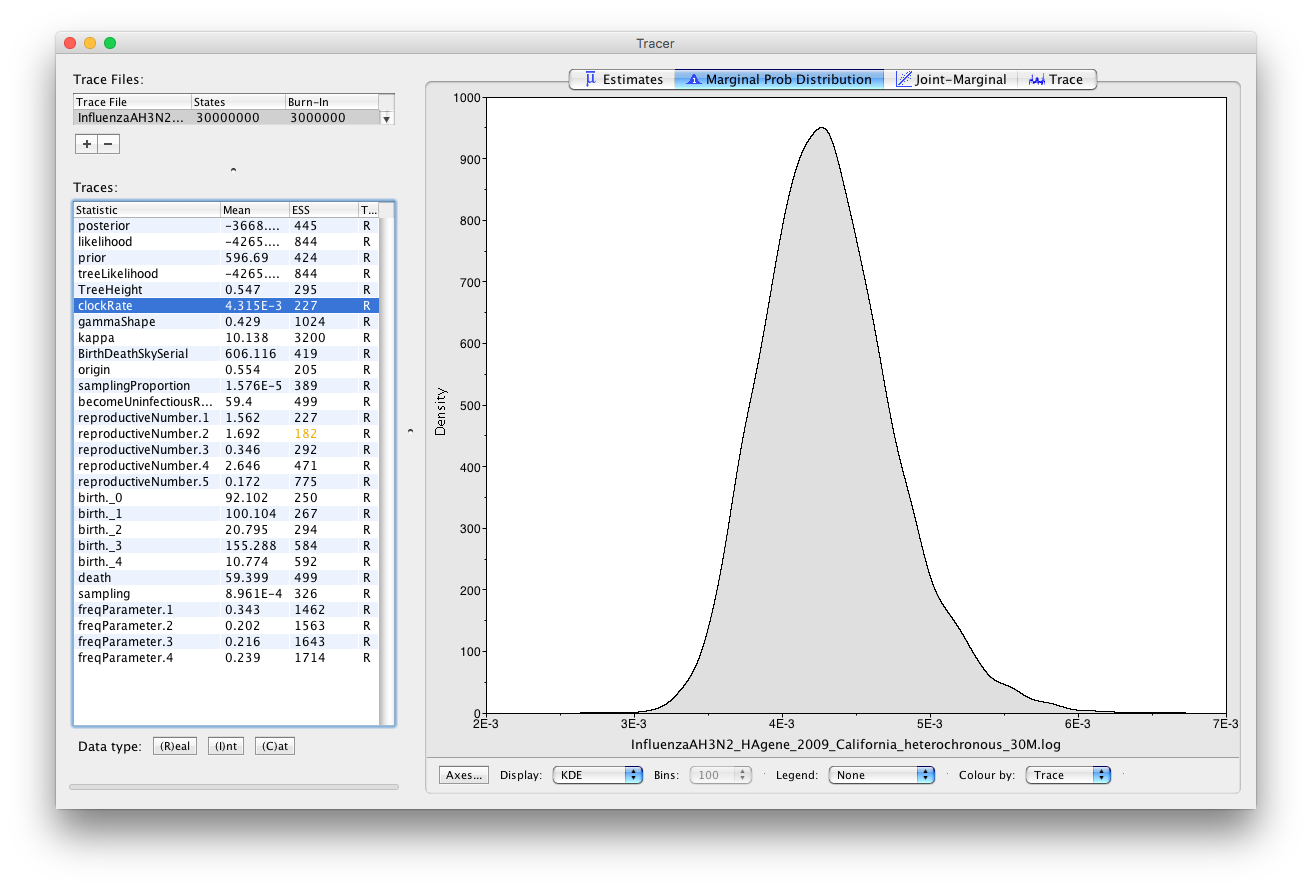
Click on clockRate and then click on Trace to examine the trace of the parameter (Figure 19).

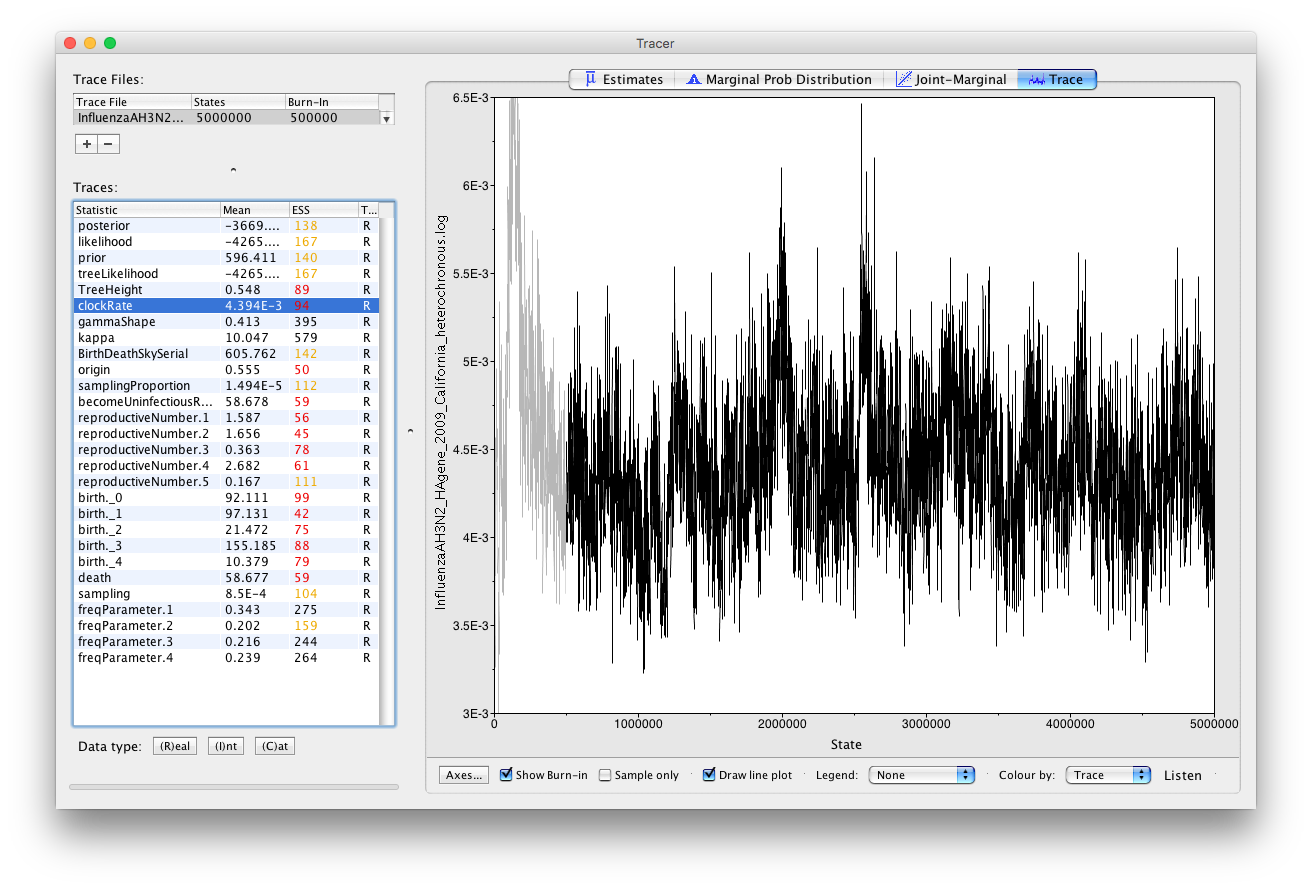
Note that even though the parameter has a low ESS, the chain appears to have passed the burn-in phase and seems to be sampling from across the posterior without getting stuck in any local optima. This is not a proof that the run is mixing well, however it gives us a good intuition that the parameter will have a good ESS value if we run the chain for longer. You should always examine the parameter traces to check convergence; a high ESS value is not proof that a run has converged to the true posterior.

If you like, you can compare your results with the example results we obtained with identical settings and a chain of 30,000,000.

Load the file InfluenzaAH3N2_HAgene_2009_California_heterochronous_30M.log.

Do the parameter traces look better?

Examine the posterior estimates for the becomeUninfectiousRate, samplingProportion and clockRate in Tracer. Do the estimates look realistic? Are they different from the priors we set and if so, how?

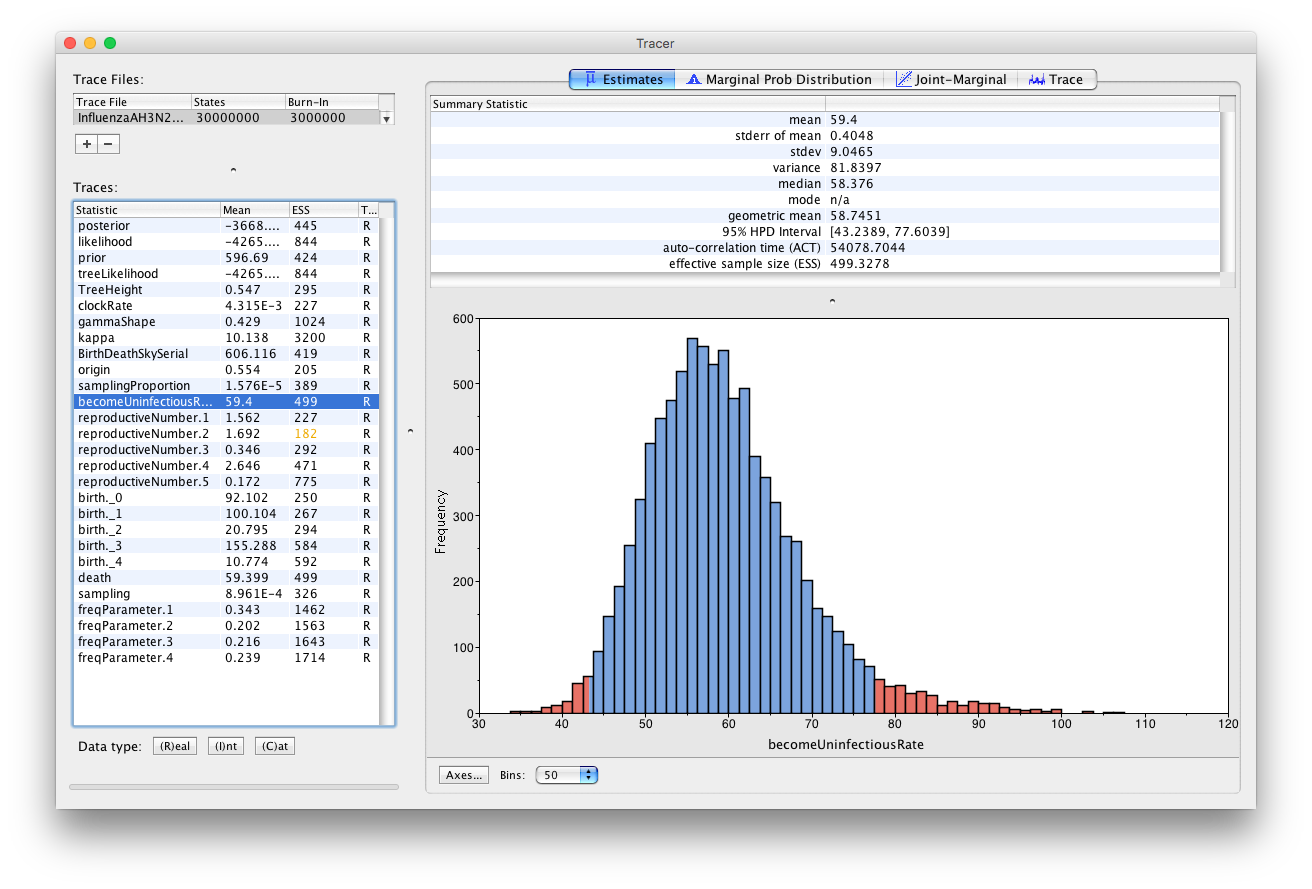
The estimated posterior distribution for the becomeUninfectiousRate has a median of 58.0557 and a 95% HPD between 44.0016 and 75.3019 (Figure 20). This is between $\approx$ 4.8 and 8.3 days, thus, roughly one week. This is a lot more specific than the prior we set, which allowed for a much longer infectious period. The estimates also agree with what we know about Influenza A. In this case there was enough information in the sequencing data to estimate a more specific becoming uninfectious rate. If we had relied more on our prior knowledge we could have set a tighter prior on the becomeUninfectiousRate parameter, which may have helped the run to converge faster, by preventing it from sampling unrealistic parameter values. However, if you are unsure about a parameter it is always better to set more diffuse priors.

We see that the sampling proportion (Figure 21) is estimated to be below $5 \times 10^{-5}$. This a lot lower than the mean we set for the prior on the sampling proportion (0.001). Therefore our prior estimate of the sampling proportion was much too high. Consequently, we see that the number of cases was also much higher than we initially thought. We assumed that there were around 1,000 cases when we set the prior, however our posterior indicates that the epidemic had on the order of tens of thousands of cases.

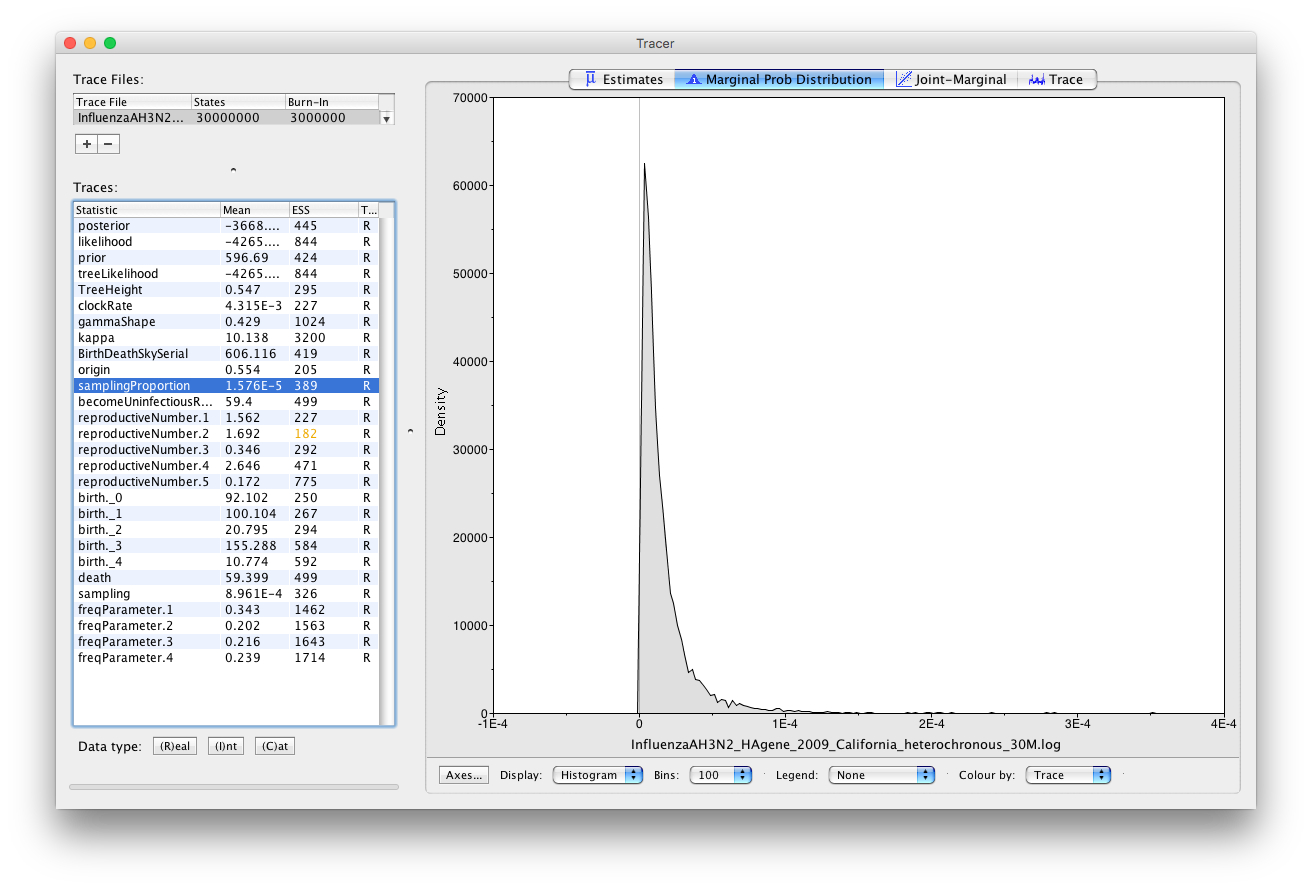
Looking at the clock rate estimates (Figure 22) we see that they are about 2 to 3 times faster than the usual substitution rate reported in (Jenkins et al., 2002) for influenza A. However, that rate was estimated for sequences from the NP (nucleocapsid) gene, while our sequences are from the HA (hemagglutinin) gene, which is a surface antigen and known to be evolving under very strong directional selection. Thus, it is expected that HA will have a faster substitution rate than NP. In addition, when viral samples are collected over a short time period the estimated clock rate is often elevated. The exact cause of the bias is not known, but it is suspected that incomplete purifying selection plays a role. What is important to keep in mind is that this is does not mean that the virus is mutating or evolving faster than usual. When samples are collected over a longer time period the estimated clock rate slows down and eventually reaches the long-term substitution rate.

Practical: H3N2 flu dynamics - Homochronous data

We could also use the homochronous data to investigate the dynamics of the H3N2 spread in California in 2009. We use the 29 sequences from April 28, 2009 to investigate whether this is possible.

Follow the same procedure as for the heterochronous sampling. Now, however, use the alignment file called InfluenzaAH3N2_HAgene_2009_California_homochronous.nexus and use the Birth Death Skyline Contemporary model as a tree prior.

Note that for the Birth Death Skyline Contemporary model the sampling proportion is called rho, and refers only to the proportion of infected individuals sampled at the present time. This is to distinguish it from the sampling proportion in the Birth Death Skyline Serial model, which refers to the proportion of individuals sampled through time.

Save the file as Homochronous.xml and run it in BEAST2.

Estimating the substitution rate from homochronous data

After the run is finished, load the log file into Tracer and examine the traces of the parameters.

Topic for discussion: Do you think running the analysis for longer will lead to it mixing well?

Most of the parameters again have ESS values below 200, however in this case the ESS values are lower than for heterochronous data and it is not clear that running the analysis for longer will lead to mixing. Indeed, while running the analysis for longer increases the ESS values for some parameters, they remain low for others, in particular the origin, TreeHeight (tMRCA) and clockRate. Low ESS values for these parameters in turn translate into low ESS values for the tree prior (BirthDeathSkyContemporary), prior and posterior.

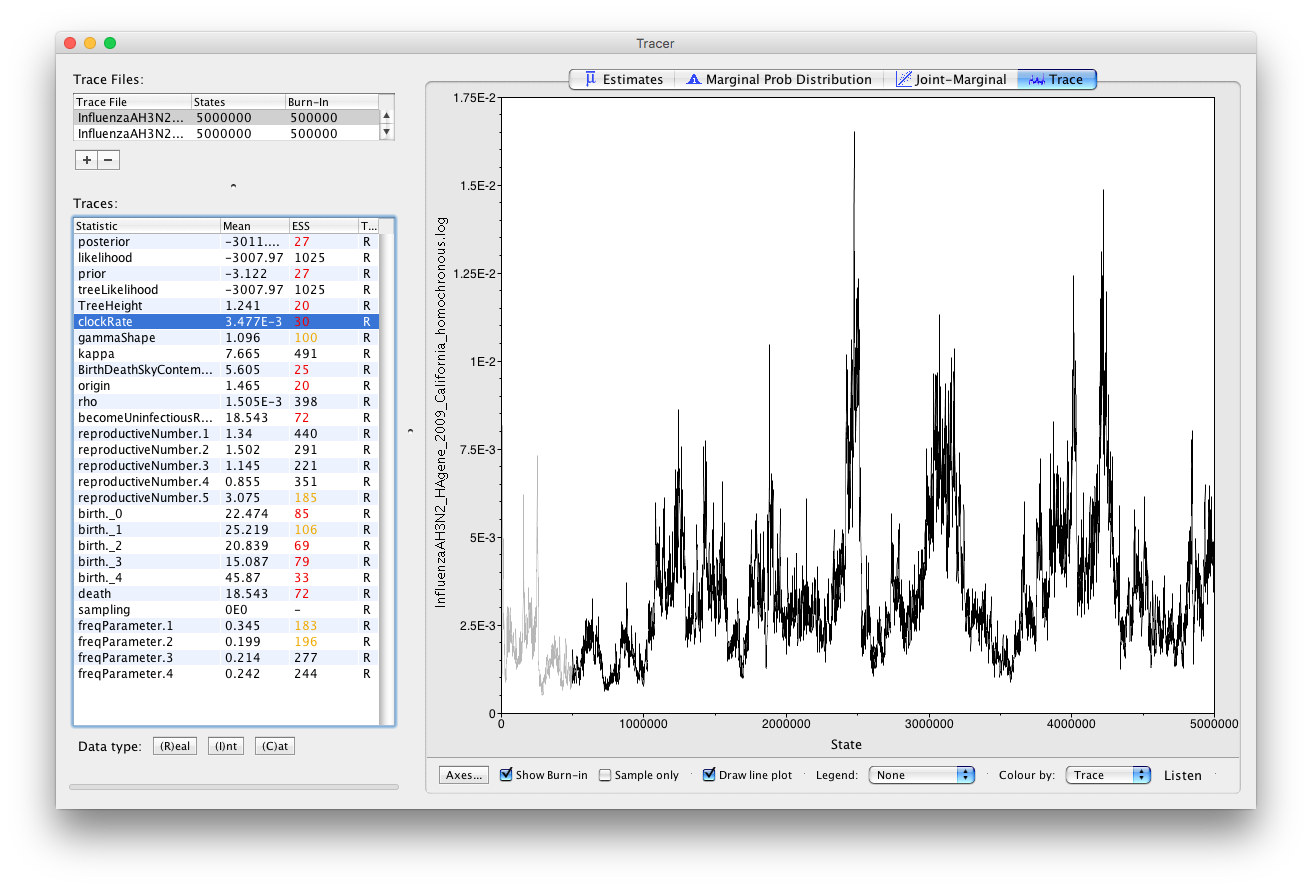
Now, check the clock rate and the tree height parameters.

Topic for discussion: Do you think that homochronous samples allow for good substitution rate estimation?

If yes, how would you know?

If not, how can you see that and where do you think might the problem be? Can we address this problem in our analysis?

Notice the values of the substitution rate estimates. From literature, one can read that influenza has a substitution rate of about $10^{-3}$ substitutions per site per year (Jenkins et al., 2002). Our estimate of the clock rate is of the same order as this value, but has a very large credible interval. Notice also, that the credible interval of the tree height is very large.

Another way to see that the homochronous sampling does not allow for the estimation of the clock rate is to observe a very strong negative correlation of the clock rate with the tree height.

In Tracer click on the Joint Marginal panel, select the TreeHeight and the clockRate simultaneously, and uncheck the Sample only box below the graphics (Figure 24).

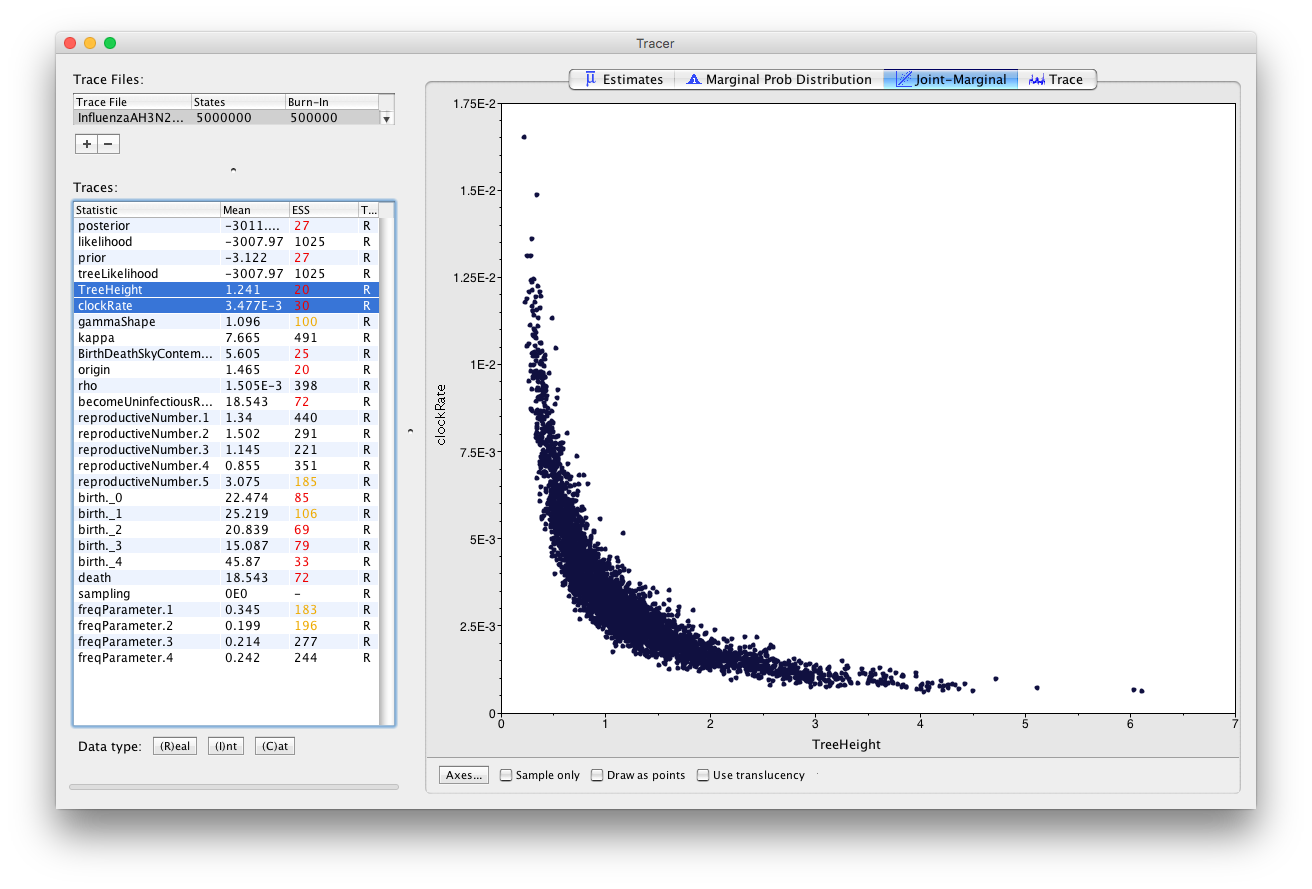
The correlation between the tree height and the clock rate is obvious: the taller the tree, the slower the clock. One way to solve this problem is to break this correlation by setting a strong prior on one of the two parameters. We describe how to set a prior on the tree height in the section below.

Topic for discussion: Are any other pairs of parameters highly correlated? If so, should we be concerned about them?

Creating Taxon Sets

We will use the results from the heterochronous data to find out what a good estimate for the tree height of these homochronous samples is. For this aim, we first create an MCC (maximum clade credibility) tree in TreeAnnotator and then check with FigTree what the estimate of the tMRCA (time to the most recent common ancestor) of the samples from April 28, 2009 is.

Note, however, that we do this for illustrative purposes only. In good practice, one should avoid re-using the data or using the results of an analysis to inform any further analyses containing the same data. Let’s pretend therefore that the heterochronous dataset is an independent dataset from the homochronous one.

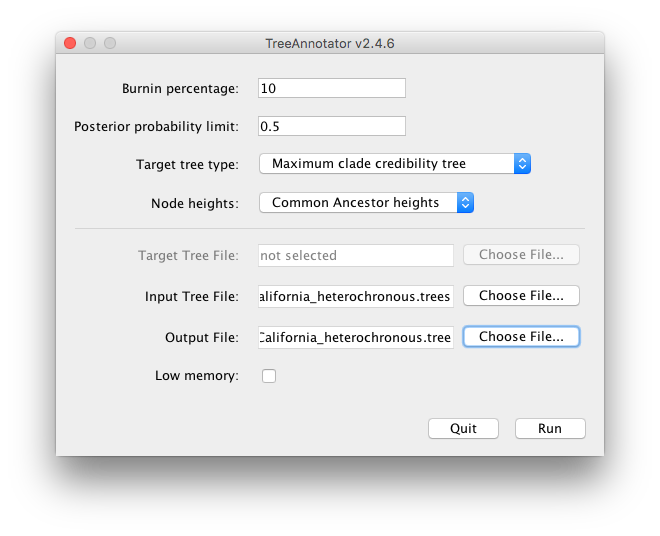
Open TreeAnnotator and set Burnin percentage to 10, Posterior probability limit to 0.5. Leave the other options unchanged.

Set the Input Tree File to InfluenzaAH3N2_HAgene_2009_California_heterochronous.trees (or drag it across) and the Output File to InfluenzaAH3N2_HAgene_2009_California_heterochronous.tree. (Figure 25)

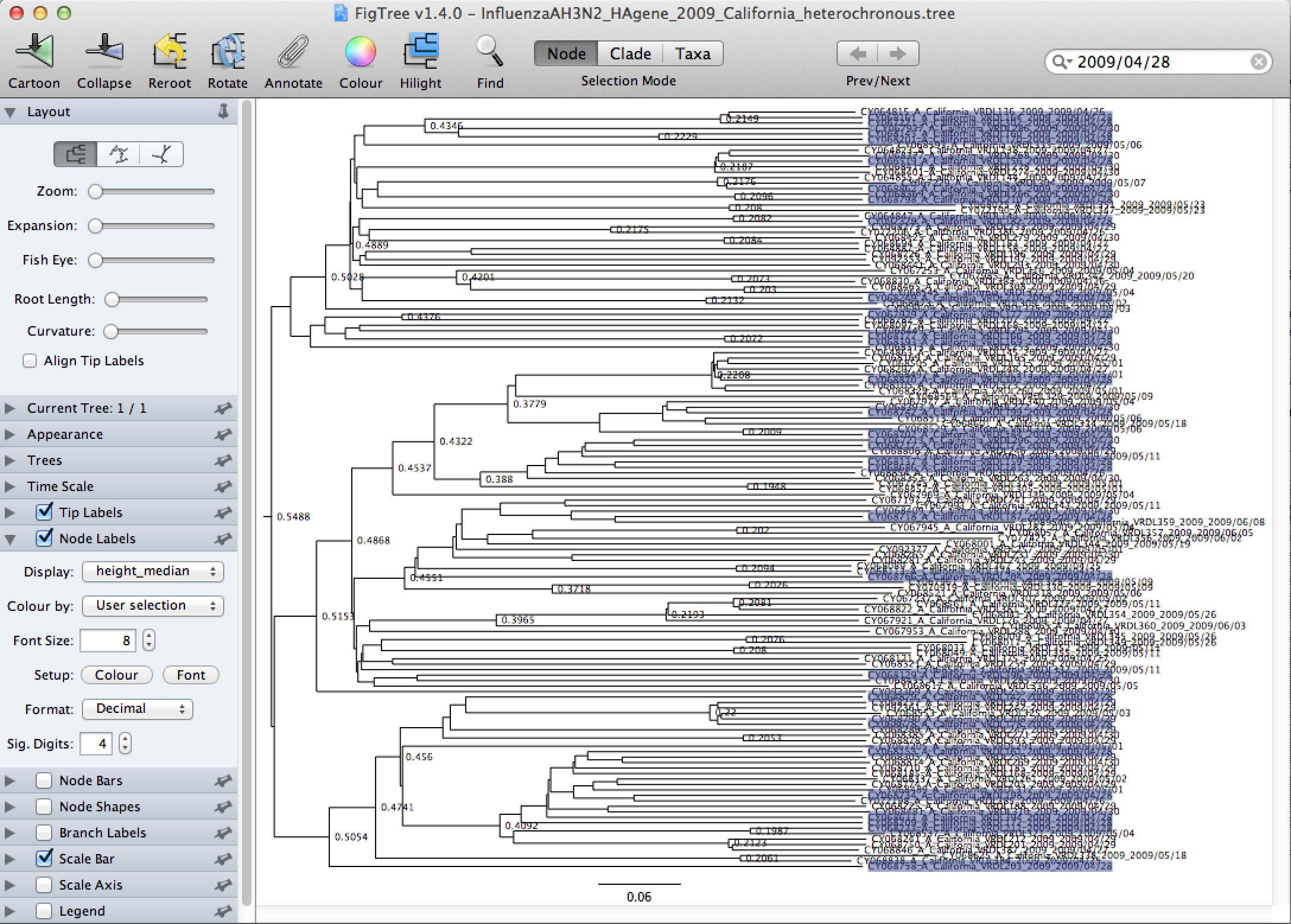
How can we find out what the tMRCA of our homochronous data may be? The best may be to have a look at the estimates of the heterochronous data in the FigTree.

Now open FigTree and load InfluenzaAH3N2_HAgene_2009_California_heterochronous.tree.

In the upper right corner, next to the magnifier glass sign, type 2009/04/28 to highlight all the sequences from April 28, 2009. (Figure 26)

Tick the Node Labels in the left menu, and click the arrow next to it to open the full options. Change the Display from age to height_median (Figure 25) and then to height_95%_HPD (Figure 27).

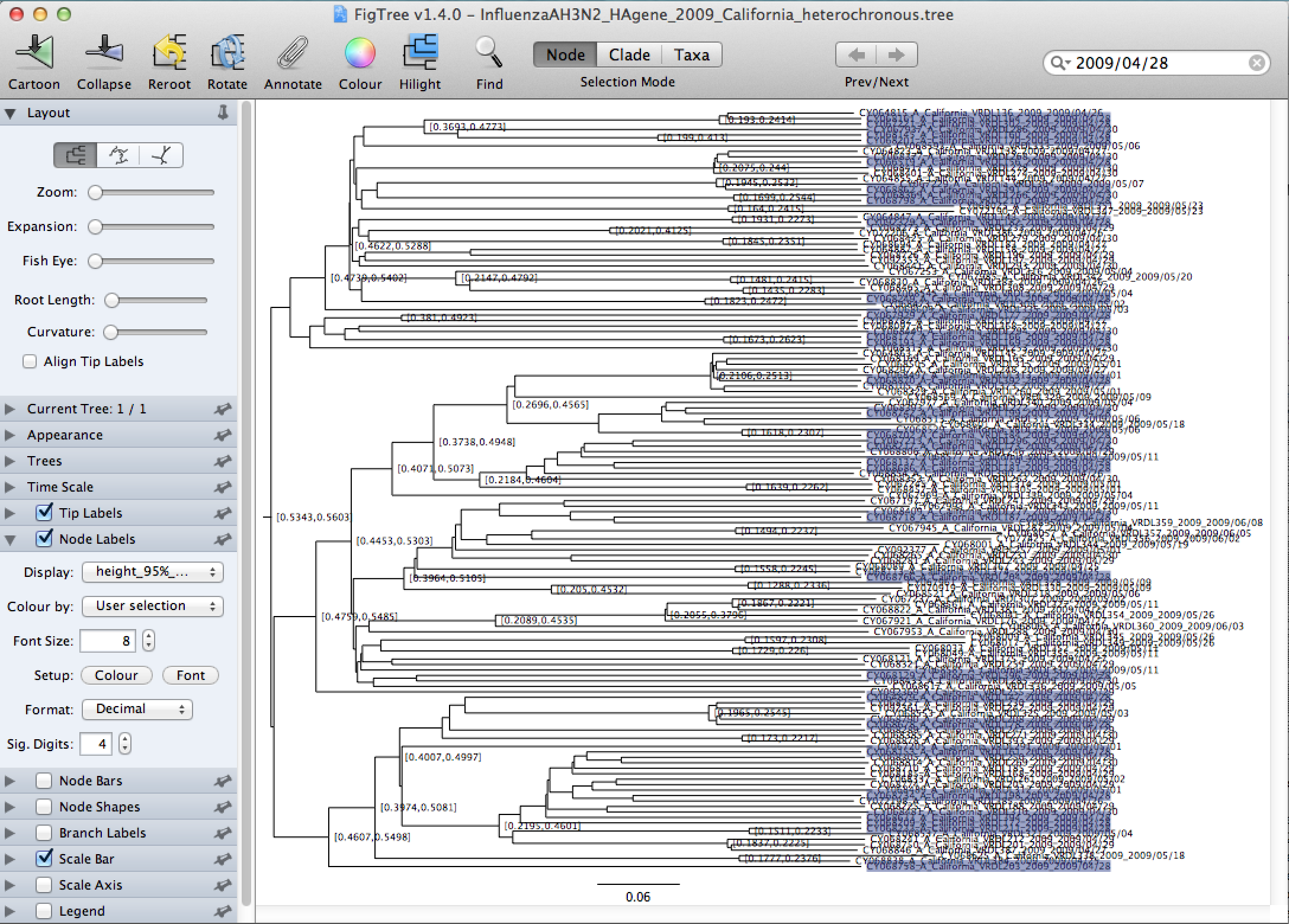
Notice, that since we are using only a subset of all the heterochronous sequences, we are interested in the tMRCA of the samples from April 28, 2009 which may not coincide with the tree height of all the heterochronous data. These samples are spread around over all the clades in the tree, and the most recent common ancestor of all of them turns out to be the root of the MCC tree of the heterochronous samples. We therefore want to set the tMRCA prior of the tree formed by the homochronous sequences to be centered around the median value of the MCC tree height, which is 0.5488 and we want 95% of the density of the prior distribution to be between 0.5343-0.5603.

Open BEAUti, load the homochronous data and use the same settings as for the Homochronous.xml file.

Create a new taxon set for root node by clicking the + Add Prior button at the bottom of the parameter list in the Priors window. Select MRCA prior in the dropdown menu (if one appears) and press OK. This will reveal the Taxon set editor.

Change the Taxon set label to allseq.

Select the sequences belonging to this clade, i.e. all the tips, and move them from the left column to the right column using the > > button and click OK. (Figure 28)

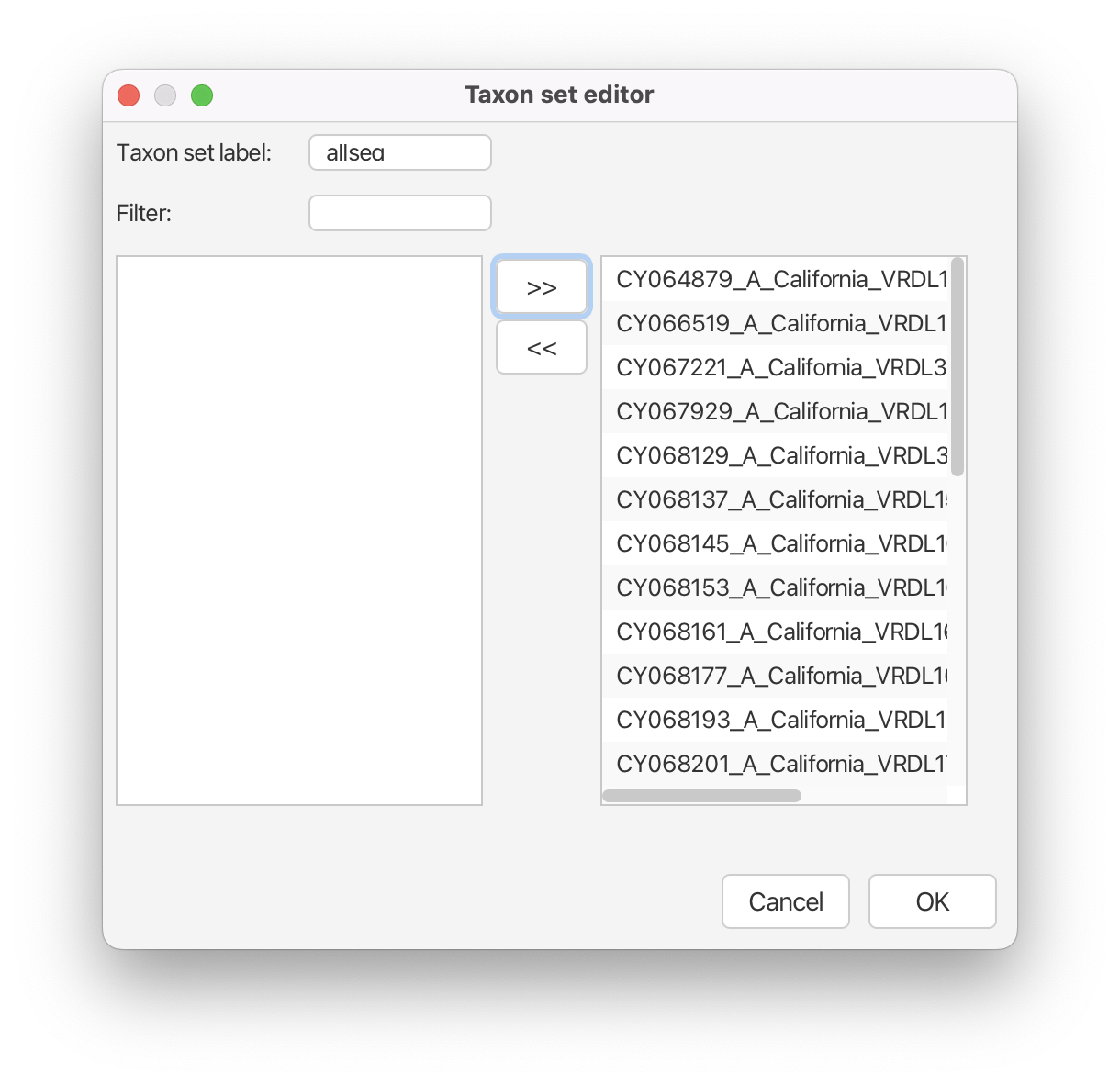
The prior that we are specifying is the date (not the height) of the tMRCA of all the samples in our dataset. Thus, we need to recalculate the date from the tMRCA height estimates that we obtained above. All the tips are sampled at the date $\approx$ 2009.3233. The median date of the MRCA should therefore be calculated as follows 2009.3233 - 0.5488 = 2008.7745 and the 95% HPD should be [2009.3233-0.5603, 2009.3233-0.5343]=[2008.763,2008.789].

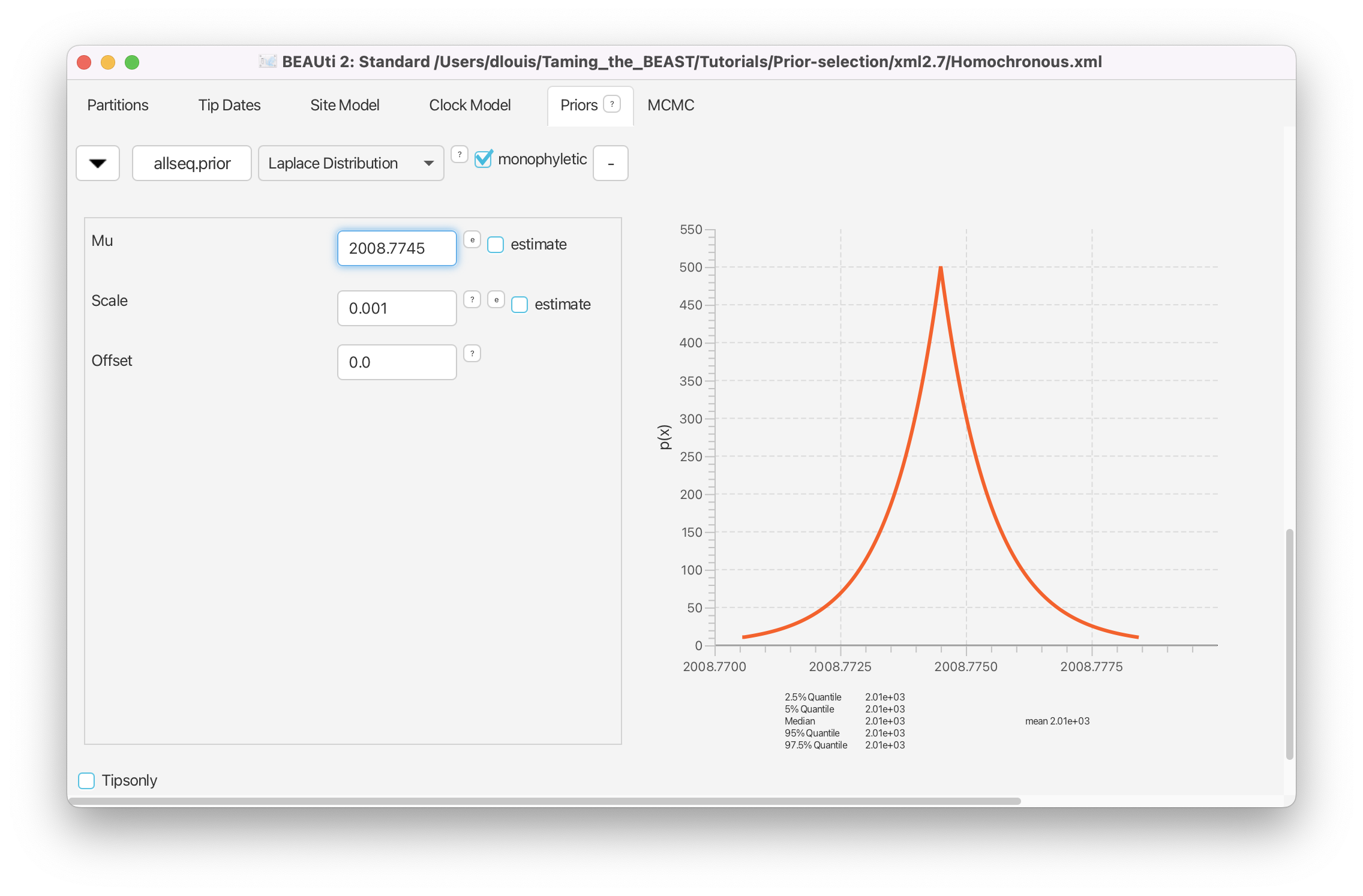
Back in the Priors window, check the box labeled monophyletic for the allseq.prior.

Click on the arrow next to the allseq.prior. Change the prior distribution on the time of the MRCA of selected sequences from [none] to Laplace Distribution and set the Mu to 2008.7745 and the Scale to 0.01 (Figure 29).

You can check that these settings correspond to the height of tMRCA from the MCC tree by setting Mu to 0.5488 and observing the distribution to the right. When you are done, do not forget to set Mu back to 2008.7745.

Save the XML file as Homochronous_tMRCA.xml and run the analysis and compare to the original analysis of the homochronous data.

Topic for discussion: Are the substitution rate estimates more precise now? What about the correlation between the tMRCA and the clock rate?

Comparison between runs

Load the log files for all three analyses into Tracer.

Select clockRate and then press shift to select all three trace files.

Click on Marginal Prob Distribution, selected Top-Right for the legend and colour by Trace File.

How do the estimates for the three analyses compare to each other?

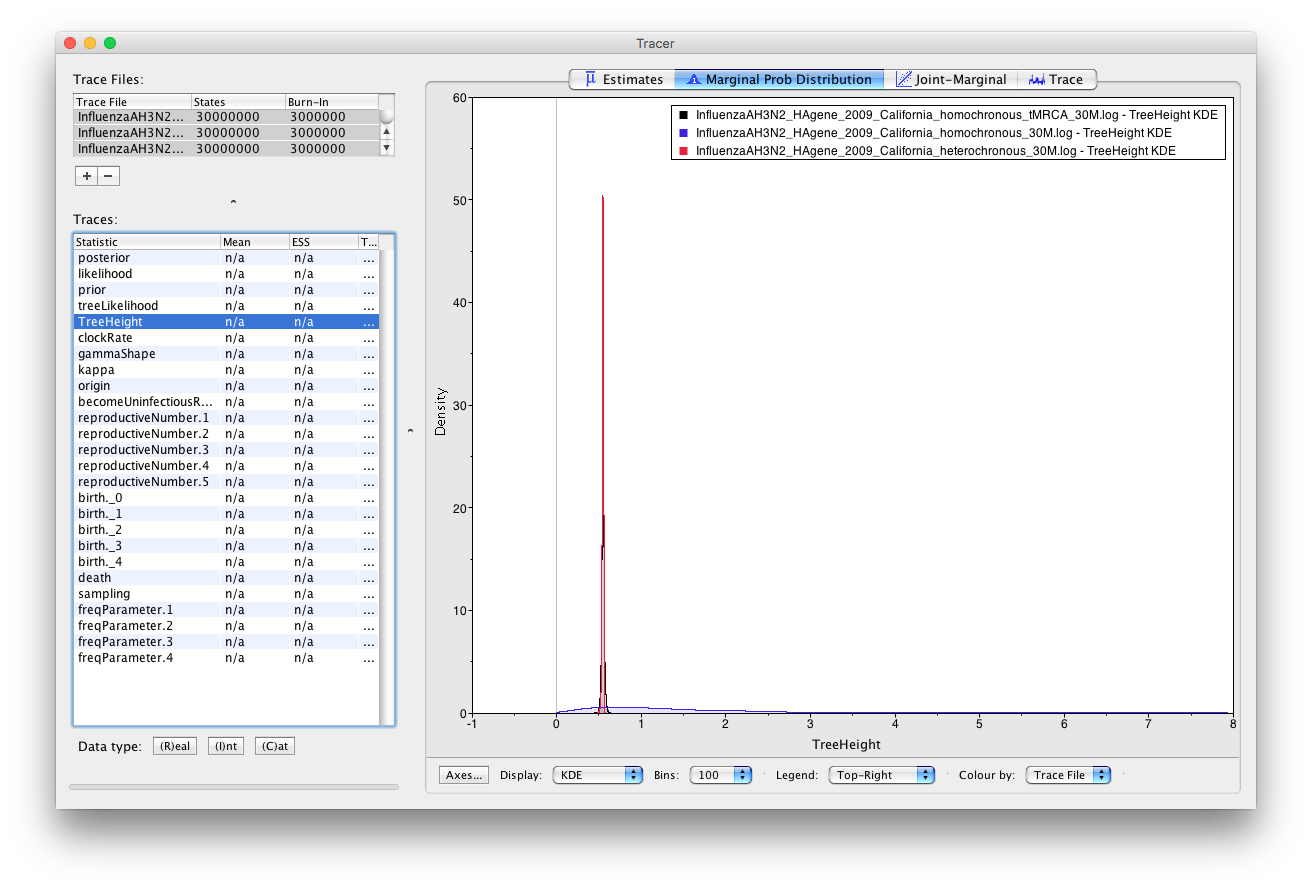
Now repeat for the TreeHeight.

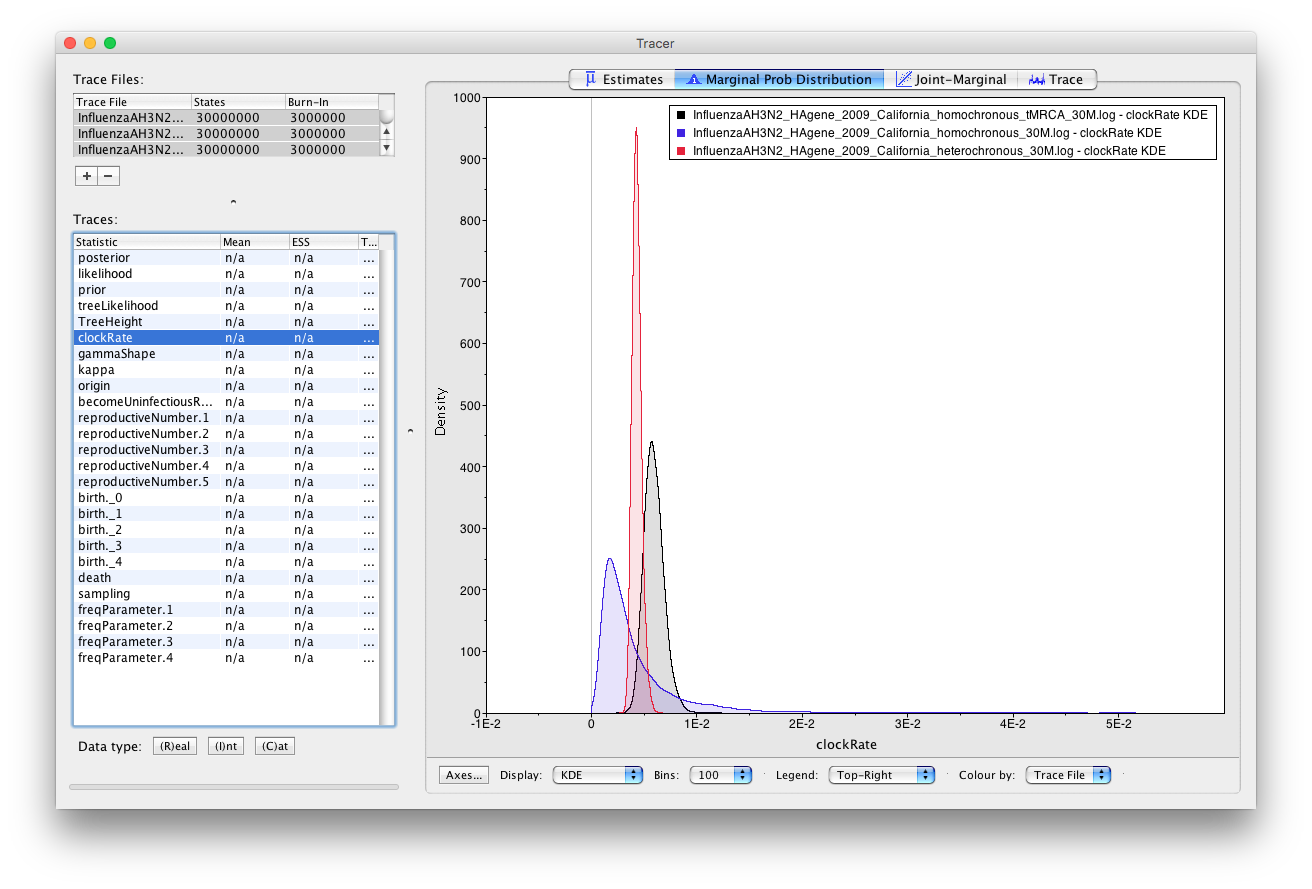
We see that the heterochronous analysis has the tightest posterior estimates for the clock rate. Hence, it is clear that this dataset contains the most information about the clock rate. This should be obvious, since this dataset not only contains sequences sampled across time, but it also contains many more sequences than the homochronous dataset. The marginal posterior for the clock rate estimated from homochronous data with a prior on the tMRCA approaches this distribution, however it is still more diffuse. On the other hand, the clock rate estimates made on the homochronous data without a tMRCA prior are very diffuse. It is important to note that these estimates are not wrong, but simply indicates that there is a lot of uncertainty in the data. Importantly, the true clock rate still falls within the 95% HPD of the estimated clock rate from homochronous data. If this were not the case then the estimates would be wrong. Thus, when there is not a lot of information in our data, it is always better to have an uncertain estimate that contains the truth than to have a very specific, but wrong estimate.

On the TreeHeight we see that the marginal posterior estimated from homochronous data with a tMRCA prior is almost identical to the marginal posterior estimated on heterochronous data. However, estimates on homochronous data without a tMRCA prior are very diffuse, because there is not enough information in the data to accurately date the tMRCA.

Note that while we can compare parameter estimates between heterochronous and homochronous data easily enough you should never compare the likelihoods or posteriors between analyses that were run on different datasets!

---

Useful Links

• Bayesian Evolutionary Analysis with BEAST 2 (Drummond & Bouckaert, 2014)
• BEAST 2 website and documentation: http://www.beast2.org/
• BEAST 1 website and documentation: http://beast.bio.ed.ac.uk
• Join the BEAST user discussion: http://groups.google.com/group/beast-users

---

Relevant References

1. Bouckaert, R., Heled, J., Kühnert, D., Vaughan, T., Wu, C.-H., Xie, D., Suchard, M. A., Rambaut, A., & Drummond, A. J. (2014). BEAST 2: A Software Platform for Bayesian Evolutionary Analysis. PLoS Computational Biology, 10(4), e1003537.
2. Bouckaert, R., Vaughan, T. G., Barido-Sottani, J., Duchêne, S., Fourment, M., Gavryushkina, A., Heled, J., Jones, G., Kühnert, D., Maio, N. D., Matschiner, M., Mendes, F. K., Müller, N. F., Ogilvie, H. A., Plessis, L. du, Popinga, A., Rambaut, A., Rasmussen, D., Siveroni, I., … Drummond, A. J. (2019). BEAST 2.5: An advanced software platform for Bayesian evolutionary analysis. PLOS Computational Biology, 15(4).
3. CDC. (2009/2010). The 2009 H1N1 Pandemic: Summary Highlights, April 2009–April 2010. Centers for Disease Control and Prevention. http://http://www.cdc.gov/h1n1flu/cdcresponse.htm
4. Stadler, T., Kühnert, D., Bonhoeffer, S., & Drummond, A. J. (2013). Birth–death skyline plot reveals temporal changes of epidemic spread in HIV and hepatitis C virus (HCV). Proceedings of the National Academy of Sciences, 110(1), 228–233.
5. Drummond, A. J., Ho, S. Y., Phillips, M. J., & Rambaut, A. (2006). Relaxed phylogenetics and dating with confidence. PLoS Biology, 4, e88.
6. Drummond, A. J., & Suchard, M. A. (2010). Bayesian random local clocks, or one rate to rule them all. BMC Biology, 8, 114.
7. Kawaoka, Y. (2006). Influenza virology: current topics. Horizon Scientific Press.
8. Jenkins, G. M., Rambaut, A., Pybus, O. G., & Holmes, E. C. (2002). Rates of molecular evolution in RNA viruses: a quantitative phylogenetic analysis. Journal of Molecular Evolution, 54(2), 156–165.
9. Drummond, A. J., & Bouckaert, R. R. (2014). Bayesian evolutionary analysis with BEAST 2. Cambridge University Press.

---

Citation

If you found Taming the BEAST helpful in designing your research, please cite the following paper:

Joëlle Barido-Sottani, Veronika Bošková, Louis du Plessis, Denise Kühnert, Carsten Magnus, Venelin Mitov, Nicola F. Müller, Jūlija Pečerska, David A. Rasmussen, Chi Zhang, Alexei J. Drummond, Tracy A. Heath, Oliver G. Pybus, Timothy G. Vaughan, Tanja Stadler (2018). Taming the BEAST – A community teaching material resource for BEAST 2. Systematic Biology, 67(1), 170–-174. doi: 10.1093/sysbio/syx060